The Satellite and Its Orbit

Cos-B was configured as a cylinder 1400 mm in diameter and 1130 mm long, with the main experiment package occupying the central region. The total mass at launch was 278 kg, of which the experiment was 118 kg.

The satellite was spin-stabilised at about 10 rpm about its axis of symmetry, which coincided with the optical axis of the gamma-ray detector. Sun and Earth sensors were used for attitude measurements from which the pointing direction could be reconstituted with a precision of about 0.5 deg. The timing accuracy was 0.5 ms or better.

The orbit of Cos-B was roughly 100 000 km with a period of 37 hours. This eccentric orbit was chosen to ensure that for most of the time the satellite was outside the Earth's radiation belts. This led to an efficient viewing programme at the price of high cosmic-ray background.

The orbital plane was inclined at roughly 90 deg to the Earth's equator and the argument of perigee was placed in the fourth quadrant to ensure that the satellite was in sight of one of the ESTRACK ground stations. Regions of the celestial sphere which are close to the direction of the line of apsides were difficult or impossible to observe, owing to the entry of the Earth into the field of view or because the Earth-aspect angle is outside the range of operation of the albedo sensors for most of the orbit. This unfortunately included the LMC and SMC for which Cos-B obtained little useful date. The right ascension of the ascending node was so chosen that these regions would not contain any target direction of high scientific interest. Unfortunately one such region proved to be Her X-1, hence Cos-B never viewed this region.

Operations and Performance

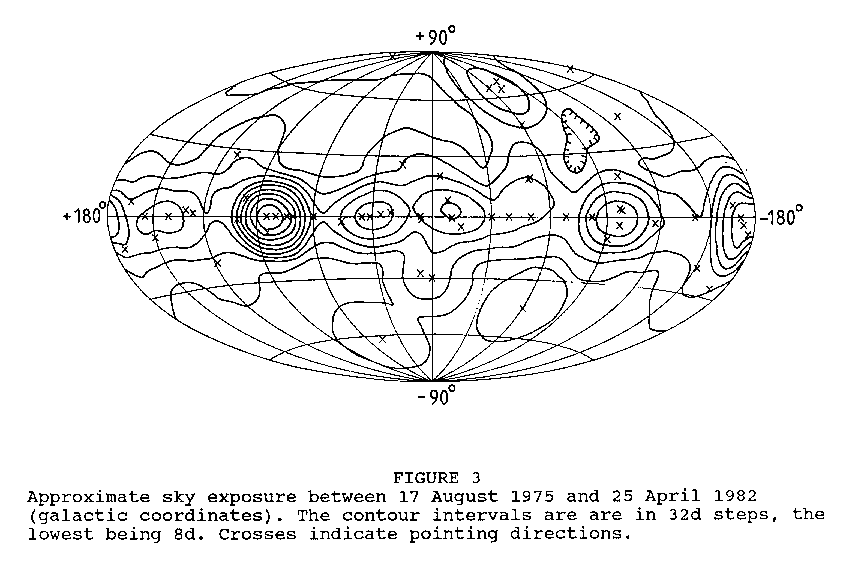
The satellite was operated in a pointing mode with its spin axis directed towards fixed points in the sky for periods of four to five weeks early in the mission and up to 3 months in later observations. In total 64 observations (or pointings) were made: the sky coverage achieved in this way is shown in Figure 3.

A broad band along the galactic equator was studied deeply, by means of repeated or overlapped observations.

About 50% of the celestial sphere was covered and about one quarter of the time was devoted to observations at higher galactic latitudes, especially regions expected to contain extragalactic sources. The experiment operated for about 25 hours in each 37-hour orbit.

The telescope performed well throughout the mission: the only complication being due to occasional erratic performance of the spark-chamber and the inevitable reduction in performance as the spark chamber gas aged. This aging was, however, minimised by means of a gas-replenishment system to permit emptying and refilling of the spark chamber. As the rate of gas deterioration decreased with time, it proved possible to increase the interval between flushing from its initial value of 6 weeks to about 36 weeks before the final flushing in November 1981. The spark chamber was still performing creditably at the end of the mission in Spring 1982.

The end of the mission coincided with the end of available attitude gas which had been conserved by careful choice of manoeuvres.

Comparison of data from overlapping observation periods enabled the longterm sensitivity changes of Cos-B to be estimated. Until three years into the mission, the sensitivity was virtually stable, but a slow fall-off developed. From this monitoring, curves such as the empirical correction factors have been derived. However the level of the background component improved with time. This background was due largely to interactions of cosmic rays with the massive parts of the experiment and surrounding spacecraft subsystems. This was reduced significantly by the increasing modulation of the cosmic rays with the approach of the solar maximum. This effect served to counter-balance the reduction in detector sensitivity.