Orbital Elements - Ulysses
The Ulysses Orbit: Classical Orbital Elements
For most applications, each phase of the Ulysses orbit is well represented by a special mathematical expression called a conic function (i.e., an ellipse or a hyperbola). In the case of the Ulysses trajectory, these are
- Earth-Jupiter segment (an ellipse)
- Jupiter fly-by (a hyperbola)
- Final out-of-ecliptic orbit (an ellipse)
The hyperbolic, Jupiter swing-by trajectory is discussed separately.
The ellipses are fully described by two quantities, namely the eccentricity and the semi-major axis (see below for their definitions).
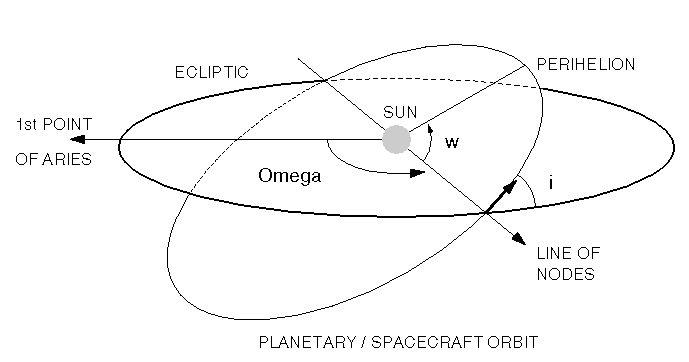
The conic functions only give the path of the spacecraft in the plane of the given part of the orbit. They tell us nothing about the orientation of the orbital plane in space. If we want to define the orbit completely, we have to use a set of parameters called the Classical Orbital Elements, which can be specified for each phase of the orbit and are usually referenced to a particular time, or epoch, and frame of reference. The definitions of the quantities making up the Classical Orbital Elements are as follows:
- Mean Distance (a) - the semi-major axis of the orbit measured in Astronomical Units (1 AU = 149.59787 million km);
- Inclination (i) - the angle between the ecliptic plane and the plane of the orbit;
- Eccentricity (e) - the eccentricity of the conic (0=circle, <1=ellipse, 1= parabola, >1=hyperbola) that describes the orbit;
- Longitude of the Ascending Node (Omega) - the position in the orbit where the path of the spacecraft passes through the ecliptic plane, from below the plane to above the plane, measured from the vernal equinox (1st point of Aries);
- Argument of Perihelion (w) - the angle in the plane of the orbit from the ascending node to the point where the spacecraft is closest to the Sun;
- Mean Anomaly (M) - angle increasing uniformly with time by 360 degrees per orbital period from 0 at perihelion;
- True Anomaly (TA) - the actual angle between the spacecraft position and the perihelion as seen from the Sun. This angle increases non-uniformly with time, changing most rapidly at perihelion.
In the case of the Ulysses orbit, the reference frame used for the orbital elements is the "Mean Ecliptic and Equinox of 1950.0".
The numerical values of the Classical Orbital Elements for the Ulysses trajectory are:
Earth-Jupiter segment (valid from 16 Oct 1990-30 Dec 1991)
a = 8.9915 AU (1345106000 km) e = 0.889166 i = 1.990719 deg. Omega = 12.85909 deg. w = 7.72595 deg. M = 0.0365574*(J - 2448177.0755) deg. where J is the Julian date of interest
Final Out-of-ecliptic Orbit (valid from 19 Mar 1992-31 Dec 2001)
a = 3.3730032 AU (504594094 km) e = 0.60306 i = 79.12801 deg. Omega = -22.51862 deg. w = -1.11377 deg. M = 0.1591096*(J - 2449788.986) deg.
In order to calculate the position of Ulysses in a given system of coordinates (e.g., heliocentric ecliptic coordinates) at a given date, we have to use the same procedure that would be needed if we wanted to know the position of a planet or comet. In general terms, this involves solving Kepler's Equation
E - e*sinE = M
to obtain an intermediate quantity called the Eccentric Anomaly E from the Mean Anomaly M. The Eccentric Anomaly E is then used to compute the True Anomaly TA, which tells us the actual position of the body (planet or spacecraft) in its orbit. Armed with this information, and the appropriate orbital elements for the Earth if needed, we can then use the other classical orbital elements to find the coordinates of Ulysses in our reference system of choice.
This general procedure is described in detail in, for example, Peter Duffett-Smith's book "Practical Astronomy with your Calculator" (3rd Edition, Cambridge, 1988), or on the World Wide Web page Planet positions using elliptical orbits
As an example, the position of Ulysses at 12:00 UT on 26 July, 1999 (Julian date 2451386.0) has been computed using the classical orbital elements listed above. The results are given in heliocentric ecliptic coordinates, heliographic Right Ascension and latitude, as well as with respect to Jupiter.
Date: 1999 07 26 12 00 00 Heliocentric Range (AU): 4.726 Xh (AU): -4.126 Yh (AU): 1.318 Zh (AU): -1.891 Heliocentric Ecliptic Lat. (deg): -23.6 Heliocentric Ecliptic Long. (deg): 162.3 Heliographic Lat. (deg): -30.8 Heliocentric Rt. Asc. (deg): 267.0 Long. with respect to Sun-Earth line (deg): 219.8 Jovicentric Range (Jupiter radii): 18751. Jovicentric Range (AU): 8.949 Jovigraphic Lat. (deg): -11.6
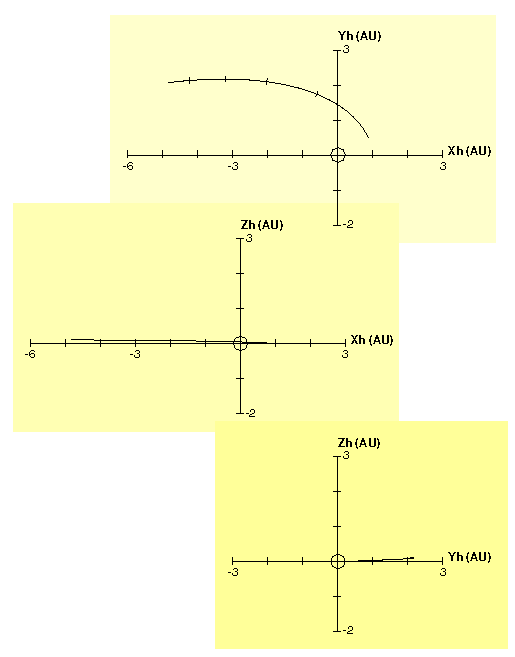
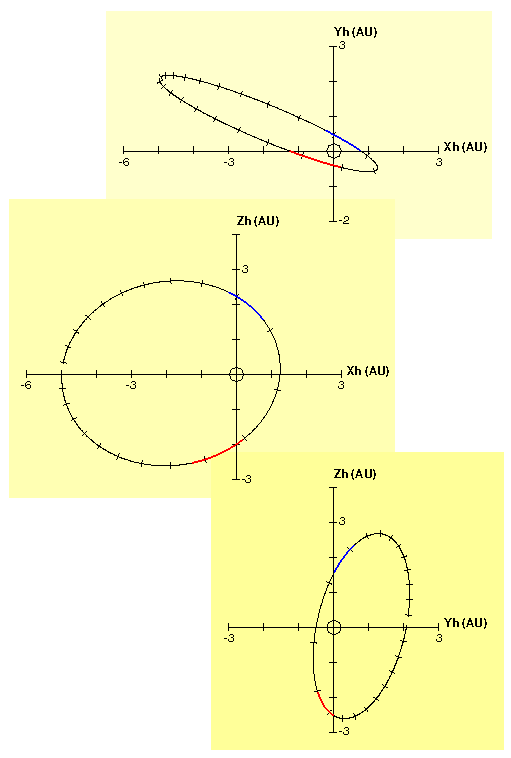
The following plots are projections of the "in-ecliptic" and "out-of-ecliptic" parts of the Ulysses orbit on the X-Y, X-Z, and Y-Z planes in heliocentric ecliptic coordinates. Tick marks are shown every 100 days. The data used to make these plots are available as ASCII files:
Earth-Jupiter segment
Final Out-of-ecliptic Orbit






































 Sign in
Sign in
 Science & Technology
Science & Technology