Gravitational Waves

Gravitational waves are ripples in the curvature of spacetime produced by a time variation of the gravitational field of massive celestial bodies. GW are characterised by an amplitude, h, which is related, at the detector side, to the change of proper distance between two spacetime events by the following relation:

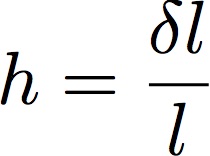
where l is the separation between the two spacetime events and δl is the variation of it caused by the passage of the GW. The above equation shows the tidal nature of the GW effects which produce length changes proportional to size. At the source side, the GW amplitude is related to the variation of the mass properties of the emitting body by the following approximate equation, called the quadrupole formula, valid for systems where the velocities are non-relativistic:

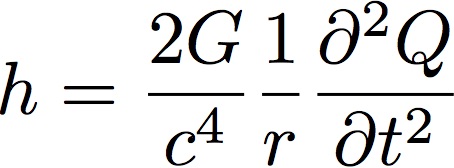
where G is the universal gravitational constant, c is the speed of light in vacuum, r is the distance from the source to the detector and Q is the quadrupole moment of the source mass distribution.

The term 2G/c⁴~10^-44 in SI units is responsible for the very low numerical value of the GW amplitude. As an example, a compact binary system comprising two 1 solar mass objects at a distance of 1kpc, gives a strain amplitude of only h~10^-22. Recalling the above equation, one can deduce that unless l is huge, the variation δl  will be very small. For future spaceborne gravitational wave detectors, such as eLISA, l is in the order of 1 million km, hence the detector must be capable of measuring δl to the order of few tens of picometres (1 picometre = 10^-12 m).

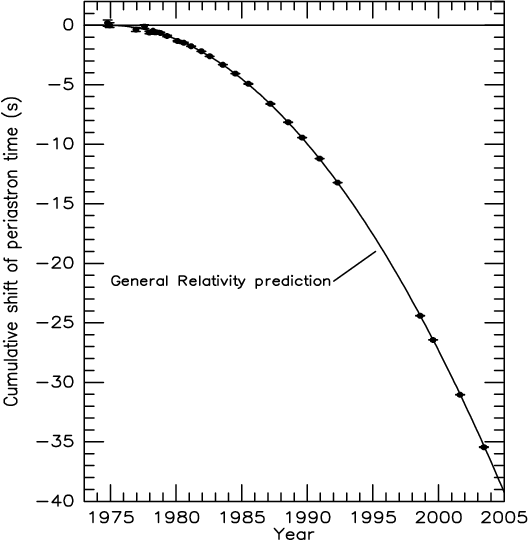
Gravitational waves are a direct consequence of Albert Einstein's theory of gravitation, or General Relativity, and the existence of gravitational radiation propagating at the speed of light was predicted by Einstein himself. Gravitational waves, as all other forms of radiation, carry energy. Especially massive and compact objects, like compact binaries and black holes at relativistic speeds emit a huge amount of radiation. This led to the first indirect detection of gravitational waves by Hulse and Taylor in 1975. They observed the inspiral of the neutron star binary pulsar PSR B1913+16 and calculated the energy loss due to escaping gravitational waves corresponding to Einstein's theory prediction to 0.3% (see figure on right).

An important feature of the gravitational waves is their frequency band. For compact sources the GW frequency band is related, through the quadrupole formula, to the source size, or lengthscale over which the source dynamics vary, and to the source mass. It can be seen that the frequency band has an upper limit at about 10⁴Hz, corresponding to emissions from very compact sources of several solar masses and Schwarzschild radius lengthscale. On the lower side, the low frequency band 10^-5 < f < 1Hz, emissions are from compact sources of thousands to millions solar masses or widely separated solar mass bodies. The GW are predicted at even much lower frequency, oscillating on scales comparable to the size of the universe. These GW have been described as "smoking gun" signature of the early universe inflation. The figure below shows in a pictorial way strain and frequency characteristics of typical eLISA sources.

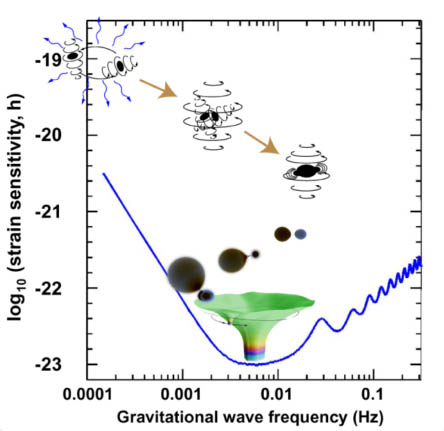
While the high frequency band is explored by ground based detectors, the low frequency GWs cannot be detected from ground, as it is impossible to completely isolate the instruments in this frequency range from local ground motions. This is the realm of the spaceborne detectors.