How to write ADQL queries for Gaia data - Gaia Users
Help supportShould you have any question, please check the Gaia FAQ section or contact the Gaia Helpdesk |
Query examples
Below is a selected sample of ADQL queries that can be executed in the Gaia ESA Archive in less than 1 minute under average user-load conditions. They are representative of different (but common) use cases. Most of them have been extracted from the different articles that accompany the Gaia (E)DR3 releases. This complementary page contains a list of Gaia Collaboration paper queries targetting all Gaia Data Releases.
Content:
- Cone search sorted by angular separation
- Cone search in galactic coordinates + DataLink filter
- Selection of rectangular sky region + 2MASS pre-computed cross-match
- Bright sources in Gaia DR2 and (E)DR3
- Basic positional cross-match: Hipparcos vs. Gaia
- Advanced positional cross-match
- Positional cross-match + proper-motion propagation
- Retrieve average quantities per HEALPix level 8 in the galactic anti-centre
- Extinction-corrected CMD diagram (histogram)
- Exploration of the interstellar medium with Gaia RVS diffuse interstellar bands
Cone search sorted by angular separation
Use case: I want to retrieve a sample of filtered sources (brighter than G=20.5 mag and with a parallax measurement) in a circular region centred on the Large Magellanic Coud [(R.A., Dec) = (81.28, -69.78) deg] with a search radius of 5 arcmin (adapted from EDR3, Gaia Collaboration, Luri et al., 2021, A&A 649, A7). The output should be ordered by the angular separation from the centre, from small to large.
Notes: Beware of integer divisions in ADQL (e.g., 5/60 = 0 whereas 5.0/60.0 = 0.083)
Target table: gaiadr3.gaia_source
Query:
SELECT *, DISTANCE(81.28, -69.78, ra, dec) AS ang_sep FROM gaiadr3.gaia_source WHERE DISTANCE(81.28, -69.78, ra, dec) < 5./60. AND phot_g_mean_mag < 20.5 AND parallax IS NOT NULL ORDER BY ang_sep ASC
Cone search in galactic coordinates + datalink filter
Use case: I want to retrieve a sample of sources contained in a circular region centred on the Small Magellanic Coud [(l, b) = (302.95, -43.98) deg] with a search radius of 5 arcmin (adapted from EDR3, Gaia Collaboration, Luri et al., 2021, A&A 649, A7) that have DataLink (see the DataLink tutorials in this page) products: epoch photometry and XP spectra.
Notes: Beware of integer divisions in ADQL (e.g., 5/60 = 0 whereas 5.0/60.0 = 0.083)
Target table: gaiadr3.gaia_source
Query:
SELECT *, DISTANCE(302.95, -43.98, l, b) AS ang_sep FROM gaiadr3.gaia_source WHERE DISTANCE(302.95, -43.98, l, b) < 5./60. AND has_epoch_photometry = 'True' AND has_xp_continuous = 'True'
SELECTION OF rectangular SKY region + 2MASS pre-computed cross-match
Use case: I want to retrieve a set of parameters from a sample of sources contained in a (projected) rectangular region centred on the Small Magellanic Cloud [(l, b) = (302.95, -43.98) deg] in Galactic coordinates, and combine them with the 2MASS Point Source Catalogue. In addition, I want to filter out the sources with lower-quality infrared photometry (according to the 2MASS PSC catalogue).
Notes: The Gaia Archive contains many pre-computed cross-matches against major surveys (see the Pre-computed cross-matches tutorial).
Target tables: gaiadr3.gaia_source, gaiadr1.tmass_original_valid, gaiadr3.tmass_psc_xsc_best_neighbour, gaiadr3.tmass_psc_xsc_join, gaiadr1.tmass_original_valid.
Query:
SELECT gaia.source_id, gaia.ra AS g_ra, gaia.dec AS g_dec, gaia.parallax, gaia.pmra, gaia.pmdec, tmass.* FROM gaiadr3.gaia_source AS gaia JOIN gaiadr3.tmass_psc_xsc_best_neighbour AS xmatch USING (source_id) JOIN gaiadr3.tmass_psc_xsc_join AS xjoin USING (clean_tmass_psc_xsc_oid) JOIN gaiadr1.tmass_original_valid AS tmass ON xjoin.original_psc_source_id = tmass.designation WHERE gaia.l BETWEEN 302.90 AND 303.00 AND gaia.b BETWEEN -44.03 AND -43.93 AND tmass.ph_qual = 'AAA'
bright sources in Gaia DR2 and (e)dr3
Use case: I want to retrieve the targets with G < 5 mag in Gaia DR2 and their Gaia DR3 counterparts (adapted from EDR3, Gaia Collaboration, Brown et al., 2021, A&A 649, A1). This query uses the pre-computed Gaia DR2-DR3 cross-match table. The output is ordered by the Gaia DR2 source_id field.
Target table: gaiadr2.gaia_source, gaiadr3.dr2_neighbourhood.
Query:
SELECT dr2.source_id, dr2.phot_g_mean_mag, dr3.* FROM gaiadr2.gaia_source AS dr2 JOIN gaiadr3.dr2_neighbourhood AS dr3 ON dr2.source_id = dr3.dr2_source_id WHERE dr2.phot_g_mean_mag < 5 ORDER BY dr2.source_id ASC
BASIC positional cross-match: hipparcos vs gaia
Use case: I want to carry out a positional cross-match between two catalogues using a cone-seach radius of 1 arcsecond (0.00028 degrees).
Notes: When cross-matching catalogues in the Gaia Archive, the smaller and larger catalogues should be used as the first and second pair of arguments of the DISTANCE function, respectively. Otherwise, the Archive response time can be degraded by several orders of magnitude - please see the Catalogue Combination tutorial for details and useful examples. The TOP 1000 introduces a bias in the output and it is only used to ensure that this query is executed in less than a minute in the Archive.
Target table: gaiadr3.gaia_source, public.hipparcos.
Query:
SELECT TOP 1000 gaia.source_id AS g_source_id, gaia.ra AS g_ra, gaia.dec AS g_dec, gaia.pmra AS g_pmra, gaia.pmdec AS g_pmdec, hip.*, DISTANCE(hip.ra, hip.de, gaia.ra, gaia.dec) AS ang_sep FROM public.hipparcos AS hip JOIN gaiadr3.gaia_source AS gaia ON DISTANCE(hip.ra, hip.de, gaia.ra, gaia.dec) < 0.00028
Advanced positional cross-match
Use case: I want to extract selected parameters from the gaiadr3.gaia_source and gaiadr3.synthetic_photometry_gspc tables for a sample contained in a circle of radius 1 deg centred on the globular cluster NGC 5139 (adapted from DR3, Gaia Collaboration, Montegriffo et al. 2022, A&A).
Notes: Epoch propagation is applied to the NGC 5139 coordinates - see the Epoch Propagation and the Proper-motion corrected cross-match for details and useful examples.
Target table: gaiadr3.gaia_source, gaiadr3.synthetic_photometry_gspc
Query:
SELECT dr3.source_id, dr3.ra, dr3.dec, dr3.pmra, dr3.pmra_error, dr3.pmdec, dr3.pmdec_error, dr3.ruwe, gspc.c_star, gspc.u_jkc_mag, gspc.u_jkc_flux, gspc.u_jkc_flux_error, gspc.u_jkc_flag, gspc.b_jkc_mag, gspc.b_jkc_flux, gspc.b_jkc_flux_error, gspc.b_jkc_flag, gspc.v_jkc_mag, gspc.v_jkc_flux, gspc.v_jkc_flux_error, gspc.v_jkc_flag, gspc.y_ps1_mag, gspc.y_ps1_flux, gspc.y_ps1_flux_error, gspc.y_ps1_flag, gspc.f606w_acswfc_mag, gspc.f606w_acswfc_flux, gspc.f606w_acswfc_flux_error, gspc.f606w_acswfc_flag FROM gaiadr3.gaia_source AS dr3 JOIN gaiadr3.synthetic_photometry_gspc AS gspc USING (source_id) WHERE DISTANCE(COORD1(EPOCH_PROP_POS(201.697,-47.479472,0.1368,-3.2400,-6.7300,234.2800,2000,2016.0)), COORD2(EPOCH_PROP_POS(201.697,-47.479472,0.1368,-3.2400,-6.7300,234.2800,2000,2016.0)), ra, dec) < 1.
positional cross-match + PROPER-MOTION propagation
Use case: I want to propagate Gaia epoch J2016.0 positions from a sample of targets (the Pleiades) to an epoch in the past for comparison against a catalogue with epoch J2000 astrometry. Matches are defined when objects are closer than 1 arcsec. The Pleiades are defined, for simplicity, using a simple cone search with a radius of 5 degrees plus a simple circular cut in proper-motion space (with a radius of 6 mas yr-1).
Notes: This query applies the built-in ADQL function "EPOCH_PROP_POS" - see the Epoch Propagation and the Proper-motion corrected cross-match for details and useful examples. The "OFFSET 0" clause increases the query performance, as it instructs the Archive PostgreSQL data base backend to respect the logical order (the subquery is executed first and other conditions applied afterwards - for more details, see this tutorial).
Target table: gaiadr3.gaia_source, external.galex_ais
Query:
SELECT subquery.source_id, subquery.parallax, subquery.phot_g_mean_mag, galex.* FROM ( SELECT gaia.*, EPOCH_PROP_POS(ra, dec, parallax, pmra, pmdec, radial_velocity, ref_epoch, 2000) AS propagated_position_vector FROM gaiadr3.gaia_source AS gaia WHERE DISTANCE(56.75, 24.12, gaia.ra, gaia.dec) < 5.0 AND SQRT(POWER(gaia.pmra - 20.5, 2) + POWER(gaia.pmdec + 45.5, 2)) < 6.0 OFFSET 0) AS subquery JOIN external.galex_ais AS galex ON DISTANCE(COORD1(subquery.propagated_position_vector), COORD2(subquery.propagated_position_vector), galex.raj2000, galex.dej2000) < 1./3600.
retrieve average quantities per healpix level 8 in the galactic anticentrE
Use case: I want to retrieve the number of stars and average quantities in all Healpixels of level 8 inside a rectangular patch on the sky (the Galactic anticentre, adapted from EDR3, Gaia Collaboration, Antoja et al., 2021, A&A 649, A8).
Target table: gaiadr3.gaia_source
Notes: The internal TOP 10000 introduces a bias in the output and it is only used to ensure that this query is executed in less than a minute in the Archive. In this example, the SQL COUNT(*) function is used in combination with the GROUP BY clause.
Query:
SELECT subquery.healpix_8, COUNT(*) AS N, AVG(phot_g_mean_mag) AS avg_g, AVG(visibility_periods_used) AS avg_vp FROM ( SELECT TOP 10000 GAIA_HEALPIX_INDEX(8, source_id) AS healpix_8, phot_g_mean_mag, visibility_periods_used FROM gaiadr3.gaia_source WHERE l < 240 AND l > 120 AND b < 60 AND b > -60 AND ruwe < 1.4 ) AS subquery GROUP BY subquery.healpix_8
EXTINCTION-CORRECTED CMD DIAGRAM (HISTOGRAM)
Use case: I want to construct a dereddened CMD diagram for a subset of stars with high-quality parallaxes (adapted from Gaia Collaboration, Andrae et al., 2018, A&A 616, A8; Fig. 19).
Notes: The random_index is an indexed field included in each gaia_source table. In this example, the constraint in the random_index is only used to ensure that the query is executed in less than 1 minute.
Target table: gaiadr3.gaia_source
Query:
SELECT bp_rp_index / 40 AS bp_rp, g_abs_index / 10 AS g_abs, n FROM ( SELECT FLOOR((bp_rp - ebpminrp_gspphot) * 40) AS bp_rp_index, FLOOR((phot_g_mean_mag - ag_gspphot + 5 * LOG10(parallax) - 10) * 10) AS g_abs_index, COUNT(*) AS n FROM gaiadr3.gaia_source WHERE parallax_over_error > 5 AND ag_gspphot IS NOT NULL AND random_index < 500000 GROUP BY bp_rp_index, g_abs_index ) AS subquery
exploration of the interstellar medium with Gaia RVS Diffuse Interstellar Bands
Use case: I want to retrieve the high-quality sample of DIBs described in the Gaia DR3 Collaboration paper "The exploration of the interstellar medium with Gaia RVS Diffuse Interstellar Bands" (Gaia Collaboration, Schultheis et al. 2022, A&A).
Notes: This query applies the "LIKE" SQL operator that allows to search for patterns (e.g., strings) in a table. The TOP 1000 introduces a bias in the output and it is only used to ensure that this query is executed in less than a minute in the Archive.
Target tables: gaiadr3.astrophysical_parameters
Query:
SELECT TOP 1000 * FROM gaiadr3.astrophysical_parameters WHERE ((flags_gspspec LIKE '0%') OR (flags_gspspec LIKE '1%')) AND ((flags_gspspec LIKE '_0%') OR (flags_gspspec LIKE '_1%')) AND ((flags_gspspec LIKE '__0%') OR (flags_gspspec LIKE '__1%')) AND ((flags_gspspec LIKE '___0%') OR (flags_gspspec LIKE '___1%')) AND ((flags_gspspec LIKE '____0%') OR (flags_gspspec LIKE '____1%')) AND ((flags_gspspec LIKE '_____0%') OR (flags_gspspec LIKE '_____1%')) AND ((flags_gspspec LIKE '______0%') OR (flags_gspspec LIKE '______1%')) AND ((flags_gspspec LIKE '_______0%') OR (flags_gspspec LIKE '_______1%')) AND ((flags_gspspec LIKE '________0%') OR (flags_gspspec LIKE '________1%')) AND ((flags_gspspec LIKE '_________0%') OR (flags_gspspec LIKE '_________1%')) AND ((flags_gspspec LIKE '__________0%') OR (flags_gspspec LIKE '__________1%')) AND ((flags_gspspec LIKE '___________0%') OR (flags_gspspec LIKE '___________1%')) AND ((flags_gspspec LIKE '____________0%') OR (flags_gspspec LIKE '____________1%'))AND (dibqf_gspspec <= 2) AND (dibqf_gspspec >= 0) AND (dib_gspspec_lambda > 862.0) AND (dib_gspspec_lambda < 862.6) AND ((dibew_gspspec_uncertainty/dibew_gspspec) < 0.35)
Query speed booster
Authors: Héctor Cánovas, Jos de Bruijne, and Alcione Mora
Writing efficient ADQL queries is not trivial and it is relatively common to introduce small mistakes or inefficiencies that significantly delay the query execution time. Fortunately, there are many tricks that boost the query performance and that can be implemented with very little effort. In most cases, these tricks can be combined to further reduce the computing time, as detailed in this intermediate level tutorial.
Tutorial content:
- Use gaia_source_lite
- Don't be lazy: don't SELECT *
- Use indexed fields + pre-computed fields + constraints
- Optimise the cross-matches
- Be careful with TOP + ORDER BY
- Randomise
- Divide and conquer
1. Use gaia_source_lite
The third Gaia data release, Gaia DR3, includes for the first time a column-wise reduced version of its main catalogue: the "gaiadr3.gaia_source_lite" table. This shortened dataset only contains 51 selected fields from the "gaiadr3.gaia_source" catalogue (click on top of the table name in the tables tree to inspect it), but the number of sources (rows) in both tables remains identical. This reduction makes it possible to substantially improve the performance of various types of ADQL queries - obviously as long as the queries do not involve fields that have been excluded from "gaiadr3.gaia_source_lite". Three representative queries that benefit from targeting this table (instead of the full table "gaiadr3.gaia_source") are listed below.
SELECT COUNT(*) FROM gaiadr3.gaia_source_lite WHERE phot_g_mean_mag <= 18.25 AND has_mcmc_msc = 'True'
SELECT ROUND(gs.logg_gspphot) AS logg, COUNT(*) FROM gaiadr3.gaia_source_lite AS gs WHERE gs.phot_g_mean_mag < 19 GROUP BY logg ORDER BY logg
SELECT COUNT(gaia.source_id) FROM gaiadr3.gaia_source_lite AS gaia INNER JOIN gaiaedr3.tmass_psc_xsc_best_neighbour AS tmass_x USING (source_id) INNER JOIN gaiadr1.tmass_original_valid AS tmass ON tmass.tmass_oid = tmass_x.clean_tmass_psc_xsc_oid INNER JOIN gaiaedr3.allwise_best_neighbour AS wise_x USING (source_id) INNER JOIN gaiadr1.allwise_original_valid AS wise USING(allwise_oid) WHERE gaia_healpix_index(5, gaia.source_id) = 1151
2. Don't be lazy: don't select *
In many situations, users only need a few fields (columns) from a catalogue for their science. But, admittedly, writing a "SELECT *" statement is way more easy than specifying one by one the list of the required fields. However, when doing so, one is forcing the database to read and store the content of all the catalogue fields per explored row. As a result, the query execution time increases significantly when analysing catalogues with many fields, like gaiadr3.gaia_source or gaiadr3.astrophysical_parameters (both contain more than 150 columns). In addition, the associated job size also increases and, in several cases, it can exceed 1 GB. This will contribute to fill up your user space (the job results quota is large but not unlimited, as explained in this FAQ). For example, the following query:
SELECT source_id, ra, dec, pmra, pmdec, parallax FROM gaiadr3.gaia_source WHERE DISTANCE(POINT(81.28, -69.78), POINT(ra, dec)) < 1
is executed in ~3 minutes, and its job size is 120 MB. The same query but selecting all fields (SELECT * ...) roughly takes 2x longer to finish and its job size is 1.1 GB. In short, we recommend to minimise the use of the SELECT * statement to execute faster queries.
3. Use indexed fields + pre-computed fields + constraints
Imagine one is interested in retrieving very blue stars in Gaia DR3. A naive way of implementing the query could be:
SELECT * FROM gaiadr3.gaia_source WHERE phot_bp_mean_mag - phot_rp_mean_mag < -2
This operation is too costly and prevents the request from being completed within the normal time-out limit. However, the same query while taking advantage of the indexed and pre-computed field bp_rp (= phot_bp_mean_mag - phot_rp_mean_mag) finishes in less than 2 minutes.
SELECT * FROM gaiadr3.gaia_source WHERE bp_rp < -2
Examples of other indexed pre-computed fields are parallax_over_error (= parallax / parallax_error), pm (=SQRT(pmra * pmra + pmdec * pmdec)), phot_g_mean_flux_over_error (= phot_g_mean_flux / phot_g_mean_flux_error), and g_rp (= phot_g_mean_mag - phot_rp_mean_mag).
In fact, part of the preparation for each Gaia data release has been the identification, creation, and indexation of the most common derived quantities to be used in queries. The information on a given field being indexed or not can be retrieved from a number of places. Probably the most convenient way is to inspect the table content using the tables tree in the Archive web interface and looking for the table fields (columns) that are highlighted in bold font, as illustrated by Fig. 2 of the Advanced (ADQL) tutorial.
Although several pre-computed fields have been added, the quantity of interest may often not be pre-computed. In those cases, adding additional restrictions based on indexed fields might be the difference between a successful and a failed (timing-out) query. For example, the following query applies constraints in the RUWE and parallax_over_error quality indicators:
SELECT phot_g_mean_mag - 5.0 * LOG10(distance_gspphot) + 5.0 AS phot_g_mean_mag_absolute, bp_rp FROM gaiadr3.gaia_source WHERE DISTANCE(POINT(266.41683, -29.00781),POINT(ra, dec)) < 2.0 -- Extra constraints AND ruwe < 1.4 AND parallax_over_error > 10.0
Excluding these two constraints delays the execution time by a factor of ~7.
4. optimise the cross-matches
Cross-matching catalogues by coordinates is one of the most common operations executed in the Gaia ESA Archive. As explained in the tutorials included in the "Combine with other data" section of the Archive Help pages, an inefficient setting of the query that launches the cross-match can increase the execution time by a factor of 3 or more. The following query retrieves the first 1000 occurrences of a geometric cross-match between Gaia DR3 and the Hipparcos catalogue, and it is executed in roughly 2.5 minutes:
SELECT TOP 1000 gaia.source_id, gaia.ra, gaia.dec, gaia.parallax, hip.* FROM public.hipparcos AS hip, gaiadr3.gaia_source AS gaia WHERE DISTANCE(POINT(gaia.ra, gaia.dec),POINT(hip.ra, hip.de)) < 1./3600
However, this conceptually similar query:
SELECT TOP 1000 gaia.source_id, gaia.ra, gaia.dec, gaia.parallax, hip.* FROM public.hipparcos AS hip JOIN gaiadr3.gaia_source AS gaia ON DISTANCE(POINT(hip.ra, hip.de),POINT(gaia.ra, gaia.dec)) < 1./3600
takes only ~5 seconds to be executed (nearly a factor 30 faster!). This is because in the second query:
- the coordinates of the smaller catalogue being cross-matched (Hipparcos in this example) are placed before the coordinates of the larger catalogue, and
- an explicit join (JOIN + ON) is used instead of an implicit one (FROM multiple tables + WHERE).
Note that, as explained in the the "Combine with other data" tutorial:
5. Be careful with top + order by
It is a common mistake to assume that relational databases (like the one behind the Gaia ESA Archive) behave like humans when exploring large catalogues. The last query in the previous example is usually executed in ~5 seconds. Let's imagine that we want to sort its output by increasing parallax, in ascending order. Probably, we would try to execute something like
SELECT TOP 1000 gaia.source_id, gaia.ra, gaia.dec, gaia.parallax, hip.* FROM public.hipparcos AS hip JOIN gaiadr3.gaia_source AS gaia ON DISTANCE(POINT(hip.ra, hip.de),POINT(gaia.ra, gaia.dec)) < 1./3600 ORDER BY parallax ASC
However, this query times out (so its execution time exceeds 2 hours) due to the combined effect of the TOP + ORDER BY clauses in the query execution plan. This is because in the backend, the database is trying to first sort the entire catalogue by random_index, and then extract the first 1000 elements. If you really want the output to be sorted by a given field, then we recommend to divide the query in two steps as follows. First, execute the query excluding the "ORDER BY <field>". Then, apply the job_upload mechanism (see the Advanced ADQL features tutorial for details) as follows:
SELECT * FROM job_upload."job<job_id>" ORDER BY <field>
The <job_id> is the unique code associated to each job (e.g., 1654361201479O) that is listed in the Jobs list area (see the Advanced (ADQL) tab tutorial for details). This last query usually finishes in a few seconds.
6. Randomise
Sometimes, using a representative random sample is sufficient to answer a scientific question. Naively, users might think to simply use the first (say) 1,000,000 rows of a table using the TOP function but this is extremely dangerous: a Postgres database does not maintain a fixed (or logical) order of the rows so use of the TOP function may lead to seriously biased results. A fixed, pre-assigned random index has therefore been introduced in a column in the main Gaia catalogues. In all cases, the column random_index runs from zero to the total number of elements (rows) minus one (and the total table size in rows can be easily found in the pop-up window of the web interface of the Archive that opens when clicking on top of the table name in the tables tree). For example, the following query shows how to construct an absolute G magnitude vs BP-RP colour diagram from a random sample extracted from Gaia DR3.
SELECT source_id, phot_g_mean_mag + 5.0 * log10(parallax) - 10.0 as g_mag_abs, bp_rp FROM gaiadr3.gaia_source_lite WHERE parallax_over_error >= 5 AND phot_bp_mean_flux_over_error > 0 AND phot_rp_mean_flux_over_error > 0 AND SQRT(POWER(2.5/log(10) / phot_bp_mean_flux_over_error, 2) + POWER(2.5/log(10) / phot_rp_mean_flux_over_error, 2)) <= 0.05 AND random_index BETWEEN 0 AND 10000000
This query usually takes ~20 minutes to be executed, and its output contains 937,877 sources. A quick TOPCAT plot is shown in the left panel of Fig. 1, showing many prominent features.
Alternatively, you may be interested in constructing a histogram to identify global trends. The following (fairly advanced) query shows how to construct the equivalent histogram with bin sizes of 0.1 in BP-RP and G absolute magnitude in two consequetive steps to minimise the query execution time:
SELECT source_id, FLOOR((phot_g_mean_mag+5.0*log10(parallax)-10.0) * 10) AS g_mag_abs_index, FLOOR(bp_rp * 10) as bp_rp_index FROM gaiadr3.gaia_source WHERE parallax_over_error >= 5 AND phot_bp_mean_flux_over_error > 0 AND phot_rp_mean_flux_over_error > 0 AND SQRT(POWER(2.5/log(10) / phot_bp_mean_flux_over_error, 2) + POWER(2.5/log(10) / phot_rp_mean_flux_over_error, 2)) <= 0.05 AND random_index BETWEEN 0 AND 10000000
followed by a query that uses the previous one (which in this example has job_id 1654361201479O) as input:
SELECT bp_rp_index / 10 AS bp_rp, g_mag_abs_index / 10 AS g_mag_abs, COUNT(*) AS n FROM job_upload.job1654361201479O GROUP BY bp_rp_index, g_mag_abs_index ORDER BY bp_rp_index, g_mag_abs_index
Execution time ~0.5 minutes; output = 5928 sources. The output of this query is shown in the right panel of Fig. 1 below.
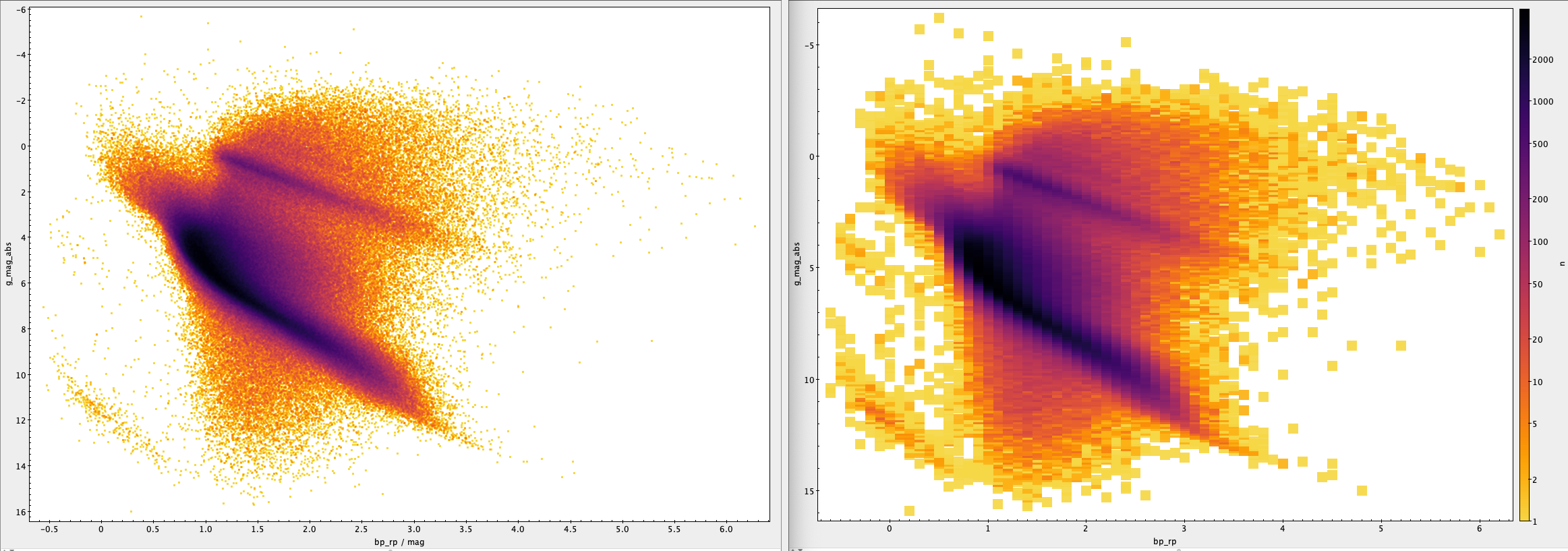
Fig. 1. Left: Colour-magnitude diagram produced with the first query in Sect. 6. Right: Histogram produced with the the second and third queries in Sect. 6. The colour bar indicates the number of sources per bin, in log scale. Both plots have been generated with TOPCAT.
7. Divide and conquer
Sometimes, a query is simply too large to be executed in one go, and the results of multiple requests need to be combined afterwards. Using the random index for chopping the query into pieces is usually advisable, to control the output size and to equalise the workload for each segment. For example, imagine we want to retrieve points for the colour-magnitude diagram shown in the previous section but for a final sample that contains ~10 million sources. The first query in Sect. 6 above retrieves roughly 1 million sources and is executed in ~20 minutes. Therefore, trying to retrieve 10 million sources in one single query will take ~200 minutes, which is beyond the query execution time limit (as explained in this FAQ). In those cases, we recommend to split the query in several chunks by random index and combine all the outputs afterwards. For example, you can run consecutive instances of the first query in Sect. 6 by simply doing a first execution using "... BETWEEN 0 AND 10000000" followed by a second one using "... BETWEEN 10000001 AND 20000000", and so on - note the BETWEEN operator includes results at both limits.
Sometimes, we are not interested in scanning a fixed number of entries in the catalogue, but a fraction. Imagine we want to scan the second 1% chunk of the catalogue in search for points for the absolute magnitude vs colour diagram. The random index can still help us when combined with the table size (remember, 1811709771 rows for gaiadr3.gaia_source):
SELECT source_id, phot_g_mean_mag + 5.0 * log10(parallax)- 10.0 as g_mag_abs, bp_rp FROM gaiadr3.gaia_source WHERE parallax_over_error >= 5 AND phot_bp_mean_flux_over_error > 0 AND phot_rp_mean_flux_over_error > 0 AND SQRT(POWER(2.5/log(10) / phot_bp_mean_flux_over_error, 2) + POWER(2.5/log(10) / phot_rp_mean_flux_over_error, 2)) <= 0.05 AND random_index BETWEEN 1 * 0.01 * 1811709771 AND 2 * 0.01 * 1811709771 - 1
Please do NOT include conditions on integer division remainders between the random_index and the fraction to explore. That is, for the previous example:
WHERE MOD(random_index, 100) = 1
Even though they are formally equivalent conditions, the data base would take a very long time and eventually fail, because an operation would be carried out on each row, instead of a quick selection on random_index values.
Alternatively, for downloads of large fractions of the dataset, we strongly recommend to make use of the bulk download repository that we offer, as explained in this tutorial. Whereas it is reasonable to launch up to a few dozen queries to collect results in chunks, as explained above, users facing the need to launch hundreds or thousands of queries are kindly advised to offload the TAP+ service and use the bulk download repository.
Ask for longer execution time quota
If all of the above advise has been tried and everything fails, and if this is the only way your science can be done, please send a motivated request to the Gaia Helpdesk with an estimate on how much additional time or user space quota is needed. Include, when possible, the offending queries because they can sometimes be optimised.
ADQL: implementation in the Gaia esa Archive
Authors: Héctor Cánovas, Jos de Bruijne, and Deborah Baines
The Astronomical Data Query Language (ADQL) is the language used by the International Virtual Observatory Alliance (IVOA) to phrase astronomical queries posted to Virtual Observatory (VO) services. ADQL is based on Structured Query Language (SQL) - a popular language to retrieve information from tables stored in a relational database. The Gaia Archive Help pages contain many tutorials and resources providing a gentle learning curve for newcomers, specially those without previous experience with SQL or relational databases. We encourage users to explore the Help pages to discover interesting use cases, advanced features, and more. The tutorials listed below are particularly useful to become familiar with the ADQL language while learning to exploit the precious data hosted by the Gaia ESA Archive:
The Gaia ESA Archive implements the latest proposed recommendation of ADQL: ADQL 2.1. Under the hood, the Archive runs PostgreSQL to manage the access to the relational database where a vast amount of data is stored. ADQL 2.1 comes with a set of mathematical and trigonometric functions (see also its Sect 2.1.4) as well as a number of optional components (see Sect. 4) that can be split into ADQL-native functions and User Defined Functions (UDF's). This document lists all the optional components that are available in the Archive (details and examples are provided in the hyper-linked document and/or in the examples below). Most of these functions are fully described (including examples shown how to use them) in the ADQL 2.1 standard, in the official PostgreSQL documentation, or in other documents available on-line. We use hyperlinks to facilitate the access to these documents whenever possible; otherwise, details and examples are provided below.
This document is structured as follows:
ADQL native components & SQL-exported functions
In addition to the optional components described in the ADQL 2.1 standard, the Archive implements a number of SQL native functions exported by the team of expert engineers and scientists working for the ESAC Science Data Centre (ESDC). These functions - labelled with an "ESDC_" prefix - are described in the official PostgreSQL documentation. A number of query examples are provided below - click on the individual hyperlinks for details.
Geometrical functions
SELECT AREA(POLYGON(POINT(246.15,-23.45), POINT(246.65,-23.45), POINT(246.4,-23.24))), COORD1(POINT(246.15,-23.45)), COORD2(POINT(246.15,-23.45)), DISTANCE(POINT(246.15,-23.45), POINT(246.65,-23.45)), INTERSECTS(CIRCLE(246.15,-23.45,0.1), CIRCLE(246.15,-23.24,0.5)) FROM dual
* As defined in the standard when the arguments are fixed values: a cross at the central position with arms extending, parallel to the coordinate axes at the centre position, for half the respective sizes on either side.
* When the arguments are variable (e.g. table columns): the sides of the box are line segments or great circles intersecting the arms of the cross in its end points at right angles with the arms.
SQL Mathematical functions
- AVG
- CBRT
- DIV
- LOG(b,x)
- ESDC_STDDEV
- SIGN
- WIDTH_BUCKET
SELECT random_index, dec, CBRT(random_index), DIV(random_index, 3), LOG(random_index, 64.0), SIGN(dec) FROM gaiadr3.gaia_source_lite WHERE random_index BETWEEN 2 AND 11
SELECT AVG(temp.dec), ESDC_STDDEV(temp.dec), WIDTH_BUCKET(AVG(temp.dec), MIN(temp.dec), MAX(temp.dec), 10) FROM (SELECT dec FROM gaiadr3.gaia_source WHERE random_index BETWEEN 0 AND 10000 ) AS temp
String functions and operators
- LOWER
- UPPER
- ILIKE
- ESDC_LEFT
- ESDC_LENGTH
- ESDC_POSITION
- ESDC_RIGHT
- ESDC_SUBSTRING
- ESDC_TRANSLATE
- ESDC_TRIM
SELECT TOP 3 designation, LOWER(designation), UPPER(designation), ESDC_LEFT(designation, 5), ESDC_RIGHT(designation, 5), ESDC_LENGTH(designation), ESDC_POSITION('DR3', designation), ESDC_SUBSTRING(designation, 3, 5), ESDC_TRANSLATE(designation, 'DR3', 'XYZ'), ESDC_TRIM(' DR3 ') FROM gaiadr3.gaia_source
SELECT TOP 10 * FROM gaiadr3.astrophysical_parameters WHERE classlabel_espels ILIKE 'ttauri'
SQL Array functions and operators
SELECT TOP 10 source_id, nss_solution_type, corr_vec, ARRAY_LENGTH(corr_vec, 1), ARRAY_DIMS(corr_vec), ARRAY_NDIMS(corr_vec), ARRAY_ELEMENT(corr_vec, 3), CARDINALITY(corr_vec) FROM gaiadr3.nss_acceleration_astro
Type operations
SELECT CAST(17.4 AS SMALLINT), CAST(1713112213.4123 AS INTEGER), CAST(1713112213.4123 AS BIGINT), CAST(91323.1231 AS REAL), CAST(91321213.112212231 AS DOUBLE),CAST('91321213.112212231' AS DOUBLE), CAST(1123 AS VARCHAR), CAST(1123 AS VARCHAR(2)), ESDC_TO_CHAR(0.0004859, '9.99EEEE'), ESDC_TO_BOOLEAN(1), ESDC_TO_BOOLEAN(0) FROM dual
Common table expressions
- WITH (this feature alows to simplify nested queries - see more details and examples in the Advanced Archive Features tutorial)
Set operators
These three operators allow to concatenate vertically the output of two or more queries (see more details and examples in the Advanced Archive Features tutorial):
CARDINALITY
CONDITIONAL FUNCTIONS
ESDC UDFs
Conditional expressions
In addition to the conditional expressions listed above, three different flavours of the PostgreSQL CASE condition have been implemented by the ESDC team:
|
Function |
PostgreSQL expression replicated |
| ESDC_IF_THEN_ELSE(condition, value, [default_value]) |
CASE WHEN condition THEN result [ELSE result] END
|
| ESDC_CASE_CONDITION(default_value, condition1, value1, condition2, value2, ...) |
CASE WHEN condition_1 THEN value_1
[WHEN ...]
else default_value
END
|
| ESDC_CASE_EXPRESSION(input_column, default_value, target_value1, value1, target_value2, value2, ...) |
CASE a
WHEN 1 THEN 'one'
[WHEN ...]
ELSE default_value
END
|
It should be noted that 'IS' and 'IN' are reserved SQL keywords. Because of this, conditions including them need to be escaped within single quotes for a correct execution in ADQL as in the general example below:
SELECT random_index,source_id, ra, dec, parallax, teff_gspphot, astrometric_params_solved, COALESCE(teff_gspphot, -1), NULLIF(astrometric_params_solved, 31), IF_THEN_ELSE('teff_gspphot is not null',1, 0) AS ite_1 , IF_THEN_ELSE('random_index in (0, 2, 4, 6, 8)', 1, 0) AS ite_2, ESDC_CASE_CONDITION(parallax, dec > 5., ra, dec < (-5.), dec) AS case_cond_1, ESDC_CASE_CONDITION('equatorial', dec > 5., 'northern', dec < (-5.), 'southern') AS case_cond_2, ESDC_CASE_EXPRESSION(astrometric_params_solved, -1, 95, 6, 31, 5, 3, 2) AS case_exp_1, ESDC_CASE_EXPRESSION(astrometric_params_solved, 'base', 95, '6p_pseudoc', 31, '5p', 3, '2p') AS case_exp_1 FROM gaiadr3.gaia_source WHERE random_index BETWEEN 0 AND 29
In addition, note that:
- ESDC_CASE_EXPRESSION does not accept column data as target values (only individual values), and
- ESDC_CASE_CONDITION does not accept individual values as output values.
Because of the above, the following query fails:
SELECT source_id, ra, dec, parallax, teff_gspphot, astrometric_params_solved, ESDC_CASE_EXPRESSION(astrometric_params_solved, source_id, 95, ra, 31, dec, 3, parallax) ESDC_CASE_CONDITION(0, dec > 5., 1, dec < (-5.), 2) FROM gaiadr3.gaia_source WHERE random_index BETWEEN 0 AND 29
Miscellaneous
The Gaia ESA Archive implements the following UDFs developed by the ESAC Science Data Centre (ESDC):
- ESDC_CROSSMATCH_POSITIONAL (table_schema_a VARCHAR, table_name_a VARCHAR, table_schema_b VARCHAR, table_name_bVARCHAR, radius DOUBLE, output_table_name VARCHAR)
- GAIA_HEALPIX_INDEX (norder INTEGER, gaia_source_id BIGINT)
ESDC_CROSSMATCH_POSITIONAL allows to execute programmatically the Archive built-in tool - see the Catalogue combination tutorial for details. The query below shows how to execute it to produce a basic cross-match (using a 1" cone-search radius) between a table that is stored in the user space and the "gaiadr3.gaia_source_lite" table:
SELECT ESDC_CROSSMATCH_POSITIONAL('user_hcanovas', 'test_esdc_xm', 'gaiadr3', 'gaia_source_lite', 1., 'unit_test') FROM dual
GAIA_HEALPIX_INDEX extracts the HEALPix level of order "norder" that is encoded in the gaia_source field:
SELECT random_index,source_id, gaia_healpix_index(7, source_id) FROM gaiadr3.gaia_source WHERE random_index BETWEEN 0 AND 9
epoch propagation
Applying epoch-propagation to a set of coordinates is far from trivial. The Gaia ESA Archive includes a number of UDFs devoted to this task. These UDFs are described in a separate Epoch Propagation tutorial.
GAVO UDFs
The following UDFs have been developed by the Gerrman Astrophysical Virtual Observatory (GAVO) and have subsequently been adopted and implemented in the Gaia ESA Archive:
- GAVO_IPIX (long REAL, lat REAL)
It returns the q3c ipix (Koposov and Bartunov, 2006) for a long/lat pair:
SELECT ra, dec, GAVO_IPIX(ra, dec) FROM gaiadr3.gaia_source WHERE random_index BETWEEN 0 AND 3
IVOA-endorsed UDFs
The following UDFs, which are described in the "Catalogue of ADQL User Defined Functions" (v1.1) endorsed note, are implemented in the Archive:
- IVO_EPOCH_PROP_POS(*)
- IVO_HASHLIST_HAS
- IVO_HASWORD
- IVO_INTERVAL_OVERLAPS
- IVO_NOCASEMATCH
- IVO_STRING_AGG
- IVO_HISTOGRAM(**)
(*) The IVO_EPOCH_PROP_POS UDF is nearly identical to the now obsolete ESDC_EPOCH_PROP_POS UDF (which will be retained for legacy purposes), with the only difference being that the output of the IVO_-prefixed UDF is serialised as an ADQL POINT (instead of a character).
In addition, the following UDFs are also available:
- IVO_GEOM_TRANSFORM
- IVO_TO_JD
- IVO_TO_MJD
- IVO_NORMAL_RANDOM
- IVO_SIMBADPOINT
Examples:
Compute the parallax histogram from a sample centred on the Pleiades:
SELECT IVO_HISTOGRAM(parallax,0.5,10.5,10) FROM gaiadr3.gaia_source_lite WHERE DISTANCE(POINT(COORD1(IVO_SIMBADPOINT('pleiades')), COORD2(IVO_SIMBADPOINT('pleiades'))), POINT(ra, dec)) < 2.0 AND parallax IS NOT NULL
(**) The array generated by the IVO_HISTOGRAM begins at position zero (array[0]), instead of position 1 (array[1]) as it happens with the rest of the arrays hosted in the Archive database. For details, see the on-line documentation of IVO_HISTOGRAM.
Select a Galactic-plane sample from the RAVE DR6 catalogue:
SELECT * FROM external.ravedr6 WHERE COORD2(IVO_GEOM_TRANSFORM('ICRS', 'GALACTIC', POINT(ra_input, dec_input))) BETWEEN -5.0 AND 5.0
*Query adapted version tested in DEV:
SELECT source_id, ra, dec, l, b, IVO_GEOM_TRANSFORM('ICRS', 'GALACTIC', POINT(ra, dec)) AS galactic_coords FROM gaiadr2.gaia_source WHERE COORD2(IVO_GEOM_TRANSFORM('ICRS', 'GALACTIC', POINT(ra, dec))) BETWEEN -5.0 AND 5.0
Select Solar System Object observations from the Gaia FPR acquired after a given date in ISO 8601 format (this UDF and the IVO_TO_MJD UDF also accept input formats like 'YYYY-MM-DDThh:mm:ss' and 'YYYY-MM-DD hh:mm:ss'). Note the 2,455,197.5 days term that is subtracted from the UDF output to follow the Gaia observations time stamping convention (see Sect. 7 in the Gaia Data Release 2 Summary paper).
SELECT * FROM gaiafpr.sso_observation WHERE epoch > (IVO_TO_JD('2020-01-01') - 2455197.5)
Generate numbers from a normal random distribution with a given mean and standard deviation (first and second arguments of the UDF, respectively):
SELECT IVO_NORMAL_RANDOM(100,3), IVO_NORMAL_RANDOM(100,50), IVO_NORMAL_RANDOM(10,1) FROM dual
Epoch Propagation
The epoch propagation algorithm used is based on the Hipparcos library released with the Hipparcos Catalogue in 1997. It implements the fully-reversible transformation of the six-element vector (position, parallax and proper motion) and its associated errors and correlation coefficients. For more information on the transformations, please refer to the official ESA 1997 SP-1200 reference document "The Hipparcos and Tycho Catalogues".
Note, the radial proper motion uncertainty is computed differently, following Michalik et al. (2014), because of its better handling of small radial velocities or parallaxes (as compared to their uncertainties).
It is also worth noting that Butkevich & Lindegren (2014) introduced more advanced epoch propagation transformations which include light-time effects. The more complicated formulae in Appendix B, which take into account light-time effects, are theoretically ideal but in practice they are not, since they cannot handle general cases of small (or even negative) parallaxes, as is possible with the "classical" formulae (Appendix C). It should be noted that the current implementation is equivalent to that of 1) Sect. 1.5.5, Vol. 1 of The Hipparcos and Tycho Catalogues (ESA 1997); 2) Michalik et al. (2014), although formulated differently, 3) Appendix C of Butkevich & Lindegren (2014), and 4) the Gaia DR3 online documentation.
These routines can be applied both to Gaia and Hipparcos data. Both catalogues use a slightly different notation for each field and a comparison table is provided in the last section. Most examples are based on Barnard's Star, having the highest proper motion, with Hipparcos and Gaia identifiers HIP 87937 and Gaia DR3 4472832130942575872. They will be based on both catalogues, when possible.
The available ADQL functions described in this section are:
- ESDC_EPOCH_PROP
- ESDC_EPOCH_PROP_POS
- ESDC_ASTROMETRIC_PARAMETERS
- ESDC_EPOCH_PROP_ERROR
- ESDC_ASTROMETRIC_PARAMETER_ERROR
- ESDC_RADIAL_VELOCITY
1. ESDC_EPOCH_PROP
This function returns the full six astrometric parameters (i.e., ra, dec, plx, pmra, pmdec, radial_pm) propagated from the reference epoch T0 to an arbitrary epoch T1. This function allows two different sets as input:
- Case 1: ESDC_EPOCH_PROP(ra,dec,plx,pmra,pmdec,rv,T0,T1):
- ra [double]: Right Ascension (deg)
- dec [double]: Declination (deg)
- plx [double]: Parallax (mas)
- pmra [double]: Proper Motion in Right Ascension (mas/yr)
- pmdec [double]: Proper Motion in Declination (mas/yr)
- rv [double]: Radial Velocity (km/s)
- T0 [double]: Reference Julian Epoch (yr)
- T1 [double]: Final Julian Epoch (yr)
The output of this function is an array (double[6]) where:
- EPOCH_PROP[1]: ra, Right Ascension (deg)
- EPOCH_PROP[2]: dec, Declination (deg)
- EPOCH_PROP[3]: plx, Parallax (mas)
- EPOCH_PROP[4]: pmra, Proper Motion in Right Ascension (mas/yr)
- EPOCH_PROP[5]: pmdec, Proper Motion in Declination (mas/yr)
- EPOCH_PROP[6]: radial_pm, Radial Proper Motion (mas/yr)
SELECT ESDC_EPOCH_PROP(ra, dec, parallax, pmra, pmdec, radial_velocity, 2016.0, 2000.0) FROM gaiadr3.gaia_source WHERE source_id = 4472832130942575872SELECT ESDC_EPOCH_PROP(ra, de, plx, pmra, pmde, -111.0, 1991.25, 2000.0) FROM public.hipparcos WHERE hip = 87937
The output parallax, pmra, pmdec, and radial proper motion are set to zero (0.0) value in case of null input parallax (which also means null input pmra and pmdec). The output radial proper motion can be a very small finite value (< 1E-04 in absolute value) if the input radial velocity is null but this value has no physical significance. The usual transformations are applied otherwise. Note this quantity is defined as radial_pm (sometimes denotes as zeta or mu_r) = radial_velocity * parallax / A, where "A" is the astronomical unit as explained in the Hipparcos reference documentation, Sec. 1.5.5. It is thus different and has different units than the radial velocity. Great care is needed to interpret the results in case of very small but non-zero parallax (below a few microarcseconds).
The output radial proper motion units are mas/yr, and it is left to the user to decide when the transformation into radial velocities in km/s is applicable, taking into account this transformation is proportional to the inverse of the parallax. To do so the dedicated function ESDC_RADIAL_VELOCITY has been implemented in the Archive.
To access the individual output array elements, the ESDC_ARRAY_ELEMENT can be used, indicating the index of the particular element as follows:
WITH p AS ( SELECT source_id, ESDC_EPOCH_PROP(ra,dec,parallax,pmra,pmdec,radial_velocity,2016.0,2000.0) AS a0, random_index FROM gaiadr3.gaia_source WHERE parallax IS NOT NULL AND radial_velocity IS NOT NULL) SELECT TOP 50 source_id, ESDC_ARRAY_ELEMENT(p.a0,1) AS ra_prop, ESDC_ARRAY_ELEMENT(p.a0,2) AS dec_prop, ESDC_ARRAY_ELEMENT(p.a0,3) AS parallax_prop, ESDC_ARRAY_ELEMENT(p.a0,4) AS pmra_prop,ESDC_ARRAY_ELEMENT(p.a0,5) AS pmdec_prop, ESDC_ARRAY_ELEMENT(p.a0,6) AS radial_pm_prop FROM pSELECT ESDC_ARRAY_ELEMENT((ESDC_EPOCH_PROP(ra,de,plx,pmra,pmde,0,1991.25,2000.0)),1) AS ra FROM public.hipparcos WHERE hip = 87937
Note that the first index in a PostgreSQL array is 1 by default.
- Case 2: ESDC_EPOCH_PROP(double[6]astrometric_parameters,T0,T1):
- double[6]astrometric parameters: astrometric parameters array, where:
- astrometric parameters[1]: ra, Right Ascension (deg)
- astrometric parameters[2]: dec, Declination (deg)
- astrometric parameters[3]: plx, Parallax (mas)
- astrometric parameters[4]: pmra, Proper Motion in Right Ascension (mas/yr)
- astrometric parameters[5]: pmde, Proper Motion in Declination (mas/yr)
- astrometric parameters[6]: rv, Radial Velocity (km/s)
- T0 [double]: Reference Julian Epoch (yr)
- T1 [double]: Final Julian Epoch (yr)
The output of this function is an array (double[6]epoch_prop) where:
- EPOCH_PROP[1]: ra, Right Ascension (deg)
- EPOCH_PROP[2]: dec, Declination (deg)
- EPOCH_PROP[3]: plx, Parallax (mas)
- EPOCH_PROP[4]: pmra, Proper Motion in Right Ascension (mas/yr)
- EPOCH_PROP[5]: pmde, Proper Motion in Declination (mas/yr)
- EPOCH_PROP[6]: radial_pm, Radial Proper Motion (mas/yr)
The astrometric parameters input array can be obtained via the ESDC_ASTROMETRIC_PARAMETERS ADQL function described below.
SELECT ESDC_EPOCH_PROP(ESDC_ASTROMETRIC_PARAMETERS(ra, dec, parallax, pmra, pmdec, radial_velocity), 2016.0, 2000.0) FROM gaiadr3.gaia_source WHERE source_id = 4472832130942575872SELECT ESDC_EPOCH_PROP(ESDC_ASTROMETRIC_PARAMETERS(ra, de, plx, pmra, pmde, -111.0), 1991.25, 2000.0) FROM public.hipparcos WHERE hip = 87937
2. ESDC_EPOCH_PROP_POS
ESDC_EPOCH_PROP_POS(ra,dec,plx,pmra,pmdec,rv,T0,T1): Returns a string with the propagated position (ra, dec) in radians from the reference epoch T0 to an arbitrary epoch T1, where:
- ra [double]: Right Ascension (deg)
- dec [double]: Declination (deg)
- plx [double]: Parallax (mas)
- pmra [double]: Proper Motion in Right Ascension (mas/yr)
- pmdec [double]: Proper Motion in Declination (mas/yr)
- rv [double]: Radial Velocity (km/s)
- T0 [double]: Reference Julian Epoch (yr)
- T1 [double]: Final Julian Epoch (yr)
This function was originally called EPOCH_PROP in Archive version 1.3.0, but has been renamed to explicitly state that only the positions are propagated, and not the full six-component vector also including parallax, proper motions, and radial velocity.
To retrieve only the Right Ascension or the Declination values in degrees from the output position of the ESDC_EPOCH_PROP function, one can use the ADQL functions COORD1 and COORD2, respectively:
SELECT COORD1(ESDC_EPOCH_PROP_POS(ra, dec, parallax, pmra, pmdec, radial_velocity, 2016.0, 2000.0)), COORD2(ESDC_EPOCH_PROP_POS(ra, dec, parallax, pmra, pmdec, radial_velocity, 2016.0, 2000.0))
FROM gaiadr3.gaia_source
WHERE source_id = 4472832130942575872
SELECT COORD1(ESDC_EPOCH_PROP_POS(ra, de, plx, pmra, pmde, -111.0, 1991.25, 2000.0)), COORD2(ESDC_EPOCH_PROP_POS(ra, de, plx, pmra, pmde, -111.0, 1991.25, 2000.0))
FROM public.hipparcos
WHERE hip = 87937
It is possible to use this function as input for other ADQL geometrical functions. For example, to compute the distance between the propagated position for a specific source and another (random) point on the sky:
SELECT DISTANCE(ESDC_EPOCH_PROP_POS(ra, dec, parallax, pmra, pmdec, radial_velocity, 2016.0, 2000.0), POINT(266.41683, -29.00781)) AS dist
FROM gaiadr3.gaia_source
WHERE source_id = 4472832130942575872
SELECT DISTANCE(ESDC_EPOCH_PROP_POS(ra, de, plx, pmra, pmde, -111.0, 1991.25, 2000), POINT(266.41683, -29.00781)) AS dist
FROM public.hipparcos
WHERE hip = 87937
3. ESDC_ASTROMETRIC_PARAMETERS
ESDC_ASTROMETRIC_PARAMETERS(ra,dec,plx,pmra,pmde,rv): Returns the full six input parameters in the correct format needed by the ESDC_EPOCH_PROP routine, where:
- ra [double]: Right Ascension (deg)
- dec [double]: Declination (deg)
- plx [double]: Parallax (mas)
- pmra [double]: Proper Motion in Right Ascension (mas/yr)
- pmde [double]: Proper Motion in Declination (mas/yr)
- rv [double]: Radial Velocity (km/s)
The output of this function is an array (double[6]astrometric_parameters) where:
- ASTROMETRIC_PARAMETERS[1]: ra (deg)
- ASTROMETRIC_PARAMETERS[2]: dec (deg)
- ASTROMETRIC_PARAMETERS[3]: plx (mas)
- ASTROMETRIC_PARAMETERS[4]: pmra (mas/yr)
- ASTROMETRIC_PARAMETERS[5]: pmde (mas/yr)
- ASTROMETRIC_PARAMETERS[6]: radial_pm (mas/yr)
SELECT ESDC_ASTROMETRIC_PARAMETERS(ra, dec, parallax, pmra, pmdec, radial_velocity)
FROM gaiadr3.gaia_source
WHERE source_id = 4472832130942575872
SELECT ESDC_ASTROMETRIC_PARAMETERS(ra, de, plx, pmra, pmde, -111.0)
FROM public.hipparcos
WHERE hip = 87937
4. esdc_EPOCH_PROP_ERROR
Returns the errors and correlation coefficients of the propagated position from the reference epoch T0 to the arbitrary epoch T1. The two index correlation matrix can be constructed from those data. Errors and correlation coefficients are used instead for convenience and consistency with the Gaia and Hipparcos catalogues. An exception is raised for input stars without a five-parameter astrometric solution, that is lacking parallaxes and proper motions. There are two accepted sets of input for this function:
- Case 1: ESDC_EPOCH_PROP_ERROR (ra, dec, plx, pmra, pmdec, rv, e_ra, e_dec, e_plx, e_pmra, e_pmdec, e_vr, de_ra, plx_ra, pmra_ra, pmde_ra, plx_de, pmra_de, pmde_de, pmra_plx, pmde_plx, pmde_pmra, T0, T1):
This transformation is only applicable for radial velocities independently determined from the astrometry, such as those obtained with a spectrometer. It is not applicable for the back-transformation of data already propagated to another epoch. The output of this function is an array with the propagated 6 errors and 15 correlation coefficients where:
SELECT ESDC_EPOCH_PROP_ERROR( ra, dec, parallax, pmra, pmdec, radial_velocity, ra_error, dec_error, parallax_error, pmra_error, pmdec_error, radial_velocity_error, ra_dec_corr, ra_parallax_corr, ra_pmra_corr, ra_pmdec_corr, dec_parallax_corr, dec_pmra_corr, dec_pmdec_corr, parallax_pmra_corr, parallax_pmdec_corr, pmra_pmdec_corr, 2016.0, 1900.0) FROM gaiadr3.gaia_source WHERE source_id = 4472832130942575872SELECT ESDC_EPOCH_PROP_ERROR( ra, de, plx, pmra, pmde, -111.0, e_radeg, e_dedeg, e_plx, e_pmra, e_pmde, 0.5, dera, plxra, pmrara, pmdera, plxde, pmrade, pmdede, pmraplx, pmdeplx, pmdepmra, 1991.25, 2000.0) FROM public.hipparcos WHERE hip = 87937For example, in order to retrieve the propagated uncertainty of the declination(e_dec) that corresponds to the second element of the array:
SELECT ESDC_ARRAY_ELEMENT((ESDC_EPOCH_PROP_ERROR( ra, dec, parallax, pmra, pmdec, radial_velocity, ra_error, dec_error, parallax_error, pmra_error, pmdec_error, radial_velocity_error, ra_dec_corr, ra_parallax_corr, ra_pmra_corr, ra_pmdec_corr, dec_parallax_corr, dec_pmra_corr, dec_pmdec_corr, parallax_pmra_corr, parallax_pmdec_corr, pmra_pmdec_corr, 2016.0, 1900.0)), 2) FROM gaiadr3.gaia_source WHERE source_id = 4472832130942575872SELECT ESDC_ARRAY_ELEMENT((ESDC_EPOCH_PROP_ERROR( ra, de, plx, pmra, pmde, -111.0, e_radeg, e_dedeg, e_plx, e_pmra, e_pmde, 0.5, dera, plxra, pmrara, pmdera, plxde, pmrade, pmdede, pmraplx, pmdeplx, pmdepmra, 1991.25, 1900.0)), 2) FROM public.hipparcos WHERE hip = 87937- ra [double]: Right Ascension (deg)
- dec [double]: Declination (deg)
- plx [double]: Parallax (mas)
- pmra [double]: Proper Motion in Right Ascension (mas/yr)
- pmdec [double]: Proper Motion in Declination (mas/yr)
- rv [double]: Radial Velocity (km/s)
- e_ra [double]: Error in Right Ascension (mas)
- e_dec [double]:Error in Declination (mas)
- e_plx [double]: Error in Parallax (mas)
- e_pmra [double]: Error in Proper Motion in RA (mas/yr)
- e_pmdec [double]: Error in Proper Motion in Dec (mas/yr)
- e_vr [double]: Error in Radial Velocity (km/s)
- de_ra [double]: Correlation Coefficient, RA/Dec
- plx_ra [double]: Correlation Coefficient, Parallax/RA
- pmra_ra [double]: Correlation Coefficient, Proper Motion in RA/RA
- pmde_ra [double]: Correlation Coefficient, Proper Motion in Dec/RA
- plx_de [double]: Correlation Coefficient, Parallax/Dec
- pmra_de [double]: Correlation Coefficient, Proper Motion in RA/Dec
- pmde_de [double]: Correlation Coefficient, Proper Motion in Dec/Dec
- pmra_plx [double]: Correlation Coefficient, Proper Motion in RA/Parallax
- pmde_plx [double]: Correlation Coefficient, Proper Motion in Dec/Parallax
- pmde_pmra [double]:Correlation Coefficient, Proper Motion in Dec/Proper Motion in RA
- T0: [double]: Reference Julian Epoch (yr)
- T1: [double]: Final Julian Epoch (yr)
- astrometric_parameter_error[1]: e_ra, Error in Right Ascension (mas)
- astrometric_parameter_error[2]: e_dec, Error in Declination (mas)
- astrometric_parameter_error[3]: e_plx, Error in Parallax (mas)
- astrometric_parameter_error[4]: e_pmra, Error in Proper Motion in RA (mas/yr)
- astrometric_parameter_error[5]: e_pmde, Error in Proper Motion in Dec(mas/yr)
- astrometric_parameter_error[6]: e_pmr, Error in Radial Proper Motion (mas/yr)
- astrometric_parameter_error[7]: de_ra, Correlation Coefficient, Dec/RA
- astrometric_parameter_error[8]: plx_ra, Correlation Coefficient, Parallax/RA
- astrometric_parameter_error[9]: pmra_ra, Correlation Coefficient, Proper Motion in RA/RA
- astrometric_parameter_error[10]: pmde_ra, Correlation Coefficient, Proper Motion in Dec/RA
- astrometric_parameter_error[11]: pmr_ra, Correlation Coefficient, Radial Proper Motion/RA
- astrometric_parameter_error[12]: plx_de, Correlation Coefficient, Parallax/Dec
- astrometric_parameter_error[13]: pmra_de, Correlation Coefficient, Proper Motion in RA/Dec
- astrometric_parameter_error[14]: pmde_de, Correlation Coefficient, Proper Motion in Dec/Dec
- astrometric_parameter_error[15]: pmr_de, Correlation Coefficient, Radial Proper Motion/Dec
- astrometric_parameter_error[16]: pmra_plx, Correlation Coefficient, Proper Motion in RA/Parallax
- astrometric_parameter_error[17]: pmde_plx, Correlation Coefficient, Proper Motion in Dec/Parallax
- astrometric_parameter_error[18]: pmr_plx, Correlation Coefficient, Radial Proper Motion/Parallax
- astrometric_parameter_error[19]: pmde_pmra, Correlation Coefficient, Proper Motion in Dec/Proper Motion in RA
- astrometric_parameter_error[20]: pmr_pmra, Correlation Coefficient, Radial Proper Motion/Proper Motion in RA
- astrometric_parameter_error[21]: pmr_pmde, Correlation Coefficient, Radial Proper Motion/Proper Motion in Dec
- Case 2: ESDC_EPOCH_PROP_ERROR(double[6] astrometric_parameters, double[21] astrometric_parameter_error, T0, T1):
This function is applicable in all cases, and makes no assumption on the correlation between the different parameters. The output of this function is an array with all the uncertainties and correlation coefficients, where:
SELECT ESDC_EPOCH_PROP_ERROR( ESDC_ASTROMETRIC_PARAMETERS(ra, dec, parallax, pmra, pmdec, radial_velocity), ESDC_ASTROMETRIC_PARAMETER_ERROR(ra_error, dec_error, parallax_error, pmra_error, pmdec_error, ra_dec_corr, ra_parallax_corr, ra_pmra_corr, ra_pmdec_corr, dec_parallax_corr, dec_pmra_corr, dec_pmdec_corr, parallax_pmra_corr, parallax_pmdec_corr, pmra_pmdec_corr, parallax, radial_velocity, radial_velocity_error), 2016.0, 1900.0) FROM gaiadr3.gaia_source WHERE source_id = 4472832130942575872SELECT ESDC_EPOCH_PROP_ERROR( ESDC_ASTROMETRIC_PARAMETERS(ra, de, plx, pmra, pmde, -111.0), ESDC_ASTROMETRIC_PARAMETER_ERROR(e_radeg, e_dedeg, e_plx, e_pmra, e_pmde, dera, plxra, pmrara, pmdera, plxde, pmrade, pmdede, pmraplx, pmdeplx, pmdepmra, plx, -111.0, 0.5), 1991.25, 1900.0) FROM public.hipparcos WHERE hip = 87937- astrometric_parameters[6] (output from ASTROMETRIC_PARAMETERS ADQL function):
- astrometric_parameters[1]: ra, Right Ascension (deg)
- astrometric_parameters[2]: dec, Declination (deg)
- astrometric_parameters[3]: plx, Parallax (mas)
- astrometric_parameters[4]: pmra, Proper Motion in Right Ascension (mas/yr)
- astrometric_parameters[5]: pmdec, Proper Motion in Declination (mas/yr)
- astrometric_parameters[6]: radial_pm, Radial Proper Motion (mas/yr)
- astrometric_parameter_error[21] (output from ASTROMETRIC_PARAMETER_ERROR ADQL function):
- astrometric_parameter_error[1]: e_ra, Error in Right Ascension (mas)
- astrometric_parameter_error[2]: e_dec, Error in Declination (mas)
- astrometric_parameter_error[3]: e_plx, Error in Parallax (mas)
- astrometric_parameter_error[4]: e_pmra, Error in Proper Motion in RA (mas/yr)
- astrometric_parameter_error[5]: e_pmdec, Error in Proper Motion in Dec(mas/yr)
- astrometric_parameter_error[6]: e_pmr, Error in Radial Proper Motion (mas/yr)
- astrometric_parameter_error[7]: de_ra, Correlation Coefficient, Dec/RA
- astrometric_parameter_error[8]: plx_ra, Correlation Coefficient, Parallax/RA
- astrometric_parameter_error[9]: pmra_ra, Correlation Coefficient, Proper Motion in RA/RA
- astrometric_parameter_error[10]: pmde_ra, Correlation Coefficient, Proper Motion in Dec/RA
- astrometric_parameter_error[11]: pmr_ra, Correlation Coefficient, Radial Proper Motion/RA
- astrometric_parameter_error[12]: plx_de, Correlation Coefficient, Parallax/Dec
- astrometric_parameter_error[13]: pmra_de, Correlation Coefficient, Proper Motion in RA/Dec
- astrometric_parameter_error[14]: pmde_de, Correlation Coefficient, Proper Motion in Dec/Dec
- astrometric_parameter_error[15]: pmr_de, Correlation Coefficient, Radial Proper Motion/Dec
- astrometric_parameter_error[16]: pmra_plx, Correlation Coefficient, Proper Motion in RA/Parallax
- astrometric_parameter_error[17]: pmde_plx, Correlation Coefficient, Proper Motion in Dec/Parallax
- astrometric_parameter_error[18]: pmr_plx, Correlation Coefficient, Radial Proper Motion/Parallax
- astrometric_parameter_error[19]: pmde_pmra, Correlation Coefficient, Proper Motion in Dec/Proper Motion in RA
- astrometric_parameter_error[20]: pmr_pmra, Correlation Coefficient, Radial Proper Motion/Proper Motion in RA
- astrometric_parameter_error[21]: pmr_pmde, Correlation Coefficient, Radial Proper Motion/Proper Motion in Dec
- T0: [double]: Reference Julian Epoch (yr)
- T1: [double]: Final Julian Epoch (yr)
- astrometric_parameter_error[1]: e_ra, Error in Right Ascension (mas)
- astrometric_parameter_error[2]: e_dec, Error in Declination (mas)
- astrometric_parameter_error[3]: e_plx, Error in Parallax (mas)
- astrometric_parameter_error[4]: e_pmra, Error in Proper Motion in RA (mas/yr)
- astrometric_parameter_error[5]: e_pmdec, Error in Proper Motion in Dec(mas/yr)
- astrometric_parameter_error[6]: e_pmr, Error in Radial Proper Motion (mas/yr)
- astrometric_parameter_error[7]: de_ra, Correlation Coefficient, Dec/RA
- astrometric_parameter_error[8]: plx_ra, Correlation Coefficient, Parallax/RA
- astrometric_parameter_error[9]: pmra_ra, Correlation Coefficient, Proper Motion in RA/RA
- astrometric_parameter_error[10]: pmde_ra, Correlation Coefficient, Proper Motion in Dec/RA
- astrometric_parameter_error[11]: pmr_ra, Correlation Coefficient, Radial Proper Motion/RA
- astrometric_parameter_error[12]: plx_de, Correlation Coefficient, Parallax/Dec
- astrometric_parameter_error[13]: pmra_de, Correlation Coefficient, Proper Motion in RA/Dec
- astrometric_parameter_error[14]: pmde_de, Correlation Coefficient, Proper Motion in Dec/Dec
- astrometric_parameter_error[15]: pmr_de, Correlation Coefficient, Radial Proper Motion/Dec
- astrometric_parameter_error[16]: pmra_plx, Correlation Coefficient, Proper Motion in RA/Parallax
- astrometric_parameter_error[17]: pmde_plx, Correlation Coefficient, Proper Motion in Dec/Parallax
- astrometric_parameter_error[18]: pmr_plx, Correlation Coefficient, Radial Proper Motion/Parallax
- astrometric_parameter_error[19]: pmde_pmra, Correlation Coefficient, Proper Motion in Dec/Proper Motion in RA
- astrometric_parameter_error[20]: pmr_pmra, Correlation Coefficient, Radial Proper Motion/Proper Motion in RA
- astrometric_parameter_error[21]: pmr_pmde, Correlation Coefficient, Radial Proper Motion/Proper Motion in Dec
- astrometric_parameters[6] (output from ASTROMETRIC_PARAMETERS ADQL function):
5. esdc_ASTROMETRIC_PARAMETER_ERROR
ESDC_ASTROMETRIC_PARAMETER_ERROR(e_ra, e_dec, e_plx, e_pmra, e_pmde, dera, plxra, pmrara, pmdera, plxde, pmrade, pmdede, pmraplx, pmdeplx, pmdepmra, plx, rv, e_rv): Returns the initial uncertainties and correlation coefficients where:
- e_ra [double]: Error in Right Ascension (mas)
- e_dec [double]:Error in Declination (mas)
- e_plx [double]: Error in Parallax (mas)
- e_pmra [double]: Error in Proper Motion in RA (mas/yr)
- e_pmdec [double]: Error in Proper Motion in Dec (mas/yr)
- de_ra [double]: Correlation Coefficient, RA/Dec
- plx_ra [double]: Correlation Coefficient, Parallax/RA
- pmra_ra [double]: Correlation Coefficient, Proper Motion in RA/RA
- pmde_ra [double]: Correlation Coefficient, Proper Motion in Dec/RA
- plx_de [double]: Correlation Coefficient, Parallax/Dec
- pmra_de [double]: Correlation Coefficient, Proper Motion in RA/Dec
- pmde_de [double]: Correlation Coefficient, Proper Motion in Dec/Dec
- pmra_plx [double]: Correlation Coefficient, Proper Motion in RA/Parallax
- pmde_plx [double]: Correlation Coefficient, Proper Motion in Dec/Parallax
- pmde_pmra [double]:Correlation Coefficient, Proper Motion in Dec/Proper Motion in RA
- plx [double]: Parallax (mas)
- rv [double]: Radial Velocity (km/s)
- e_rv [double]: Error in Radial Velocity (km/s)
The output of this function is an array (double[21] astrometric_parameters_error) with all the uncertainties and correlation coefficients, where:
- esdc_astrometric_parameter_error[1]: e_ra, Error in Right Ascension (mas)
- esdc_astrometric_parameter_error[2]: e_dec, Error in Declination (mas)
- esdc_astrometric_parameter_error[3]: e_plx, Error in Parallax (mas)
- esdc_astrometric_parameter_error[4]: e_pmra, Error in Proper Motion in RA (mas/yr)
- esdc_astrometric_parameter_error[5]: e_pmde, Error in Proper Motion in Dec (mas/yr)
- esdc_astrometric_parameter_error[6]: e_pmr, Error in Radial Proper Motion (mas/yr)
- esdc_astrometric_parameter_error[7]: de_ra, Correlation Coefficient, Dec/RA
- esdc_astrometric_parameter_error[8]: plx_ra, Correlation Coefficient, Parallax/RA
- esdc_astrometric_parameter_error[9]: pmra_ra, Correlation Coefficient, Proper Motion in RA/RA
- esdc_astrometric_parameter_error[10]: pmde_ra, Correlation Coefficient, Proper Motion in Dec/RA
- esdc_astrometric_parameter_error[11]: pmr_ra, Correlation Coefficient, Radial Proper Motion/RA
- esdc_astrometric_parameter_error[12]: plx_de, Correlation Coefficient, Parallax/Dec
- esdc_astrometric_parameter_error[13]: pmra_de, Correlation Coefficient, Proper Motion in RA/Dec
- esdc_astrometric_parameter_error[14]: pmde_de, Correlation Coefficient, Proper Motion in Dec/Dec
- esdc_astrometric_parameter_error[15]: pmr_de, Correlation Coefficient, Radial Proper Motion/Dec
- esdc_astrometric_parameter_error[16]: pmra_plx, Correlation Coefficient, Proper Motion in RA/Parallax
- esdc_astrometric_parameter_error[17]: pmde_plx, Correlation Coefficient, Proper Motion in Dec/Parallax
- esdc_astrometric_parameter_error[18]: pmr_plx, Correlation Coefficient, Radial Proper Motion/Parallax
- esdc_astrometric_parameter_error[18]: pmde_pmra, Correlation Coefficient, Proper Motion in Dec/Proper Motion in RA
- esdc_astrometric_parameter_error[20]: pmr_pmra, Correlation Coefficient, Radial Proper Motion/Proper Motion in RA
- esdc_astrometric_parameter_error[21]: pmr_pmde, Correlation Coefficient, Radial Proper Motion/Proper Motion in Dec
SELECT ESDC_ASTROMETRIC_PARAMETER_ERROR(
ra_error, dec_error, parallax_error, pmra_error, pmdec_error,
ra_dec_corr, ra_parallax_corr, ra_pmra_corr, ra_pmdec_corr, dec_parallax_corr, dec_pmra_corr, dec_pmdec_corr, parallax_pmra_corr, parallax_pmdec_corr, pmra_pmdec_corr,
parallax, radial_velocity, radial_velocity_error)
FROM gaiadr3.gaia_source
WHERE source_id = 4472832130942575872
SELECT ESDC_ASTROMETRIC_PARAMETER_ERROR(
e_radeg, e_dedeg, e_plx, e_pmra, e_pmde,
dera, plxra, pmrara, pmdera, plxde, pmrade, pmdede, pmraplx, pmdeplx, pmdepmra,
plx, -111.0, 0.5)
FROM public.hipparcos
WHERE hip = 87937
6. ESDC_RADIAL_VELOCITY
ESDC_RADIAL_VELOCITY(radial_pm, parallax): It provides the transformation of the radial proper motion (mas/yr) into a radial velocity (km/s), where:
- radial_pm [mas/yr]: Radial proper motion
- parallax [mas]: Parallax
This transformation is required for converting the output radial proper motion returned from the ESDC_EPOCH_PROP routine into a radial velocity in km/s where:
radial_velocity[km/s] = radial_pm[mas/yr] * A / parallax[mas], where A is the astronomical unit.
It should be noted that this transformation is inversely proportional to the input parallax, so special care should be taken for close-to-zero values in this parameter.
SELECT source_id, ESDC_ARRAY_ELEMENT(a0,1) AS ra_prop,ESDC_ARRAY_ELEMENT(a0,2) AS dec_prop,ESDC_ARRAY_ELEMENT(a0,3) AS parallax_prop,ESDC_ARRAY_ELEMENT(a0,4) AS pmra_prop,
ESDC_ARRAY_ELEMENT(a0,5) AS pmdec_prop,ESDC_RADIAL_VELOCITY(array_element(a0,6),array_element(a0,3)) AS rv_prop
FROM (
SELECT TOP 50 source_id, ESDC_EPOCH_PROP(ra, dec, parallax, pmra, pmdec, radial_velocity, 2016.0, 2000.0) AS a0
FROM gaiadr3.gaia_source
WHERE parallax IS NOT NULL AND radial_velocity IS NOT NULL) AS p
The following table provides a list of all astrometric parameters in the Gaia and Hipparcos catalogues. The corresponding tables are gaiadr3.gaia_source and public.hipparcos or public.hipparcos_newreduction.
|
Gaia |
Hipparcos |
Parameter |
Unit |
|---|---|---|---|
|
ra |
ra |
Right Ascension |
deg |
|
dec |
de |
Declination |
deg |
|
parallax |
plx |
Parallax |
mas |
|
pmra |
pmra |
Proper Motion in Right Ascension |
mas/yr |
|
pmdec |
pmde |
Proper Motion in Declination |
mas/yr |
|
radial_velocity |
|
Radial velocity |
km/s |
|
ra_error |
e_radeg |
Error in Right Ascension |
mas |
|
dec_error |
e_dedeg |
Error in Declination |
mas |
|
parallax_error |
e_plx |
Error in Parallax |
mas |
|
pmra_error |
e_pmra |
Error in Proper Motion in RA |
mas/yr |
|
pmdec_error |
e_pmde |
Error in Proper Motion in Dec |
mas/yr |
|
radial_velocity_error |
|
Error in Radial velocity |
km/s |
|
ra_dec_corr |
dera |
Correlation Coefficient, Dec/RA |
|
|
ra_parallax_corr |
plxra |
Correlation Coefficient, Parallax/RA |
|
|
ra_pmra_corr |
pmrara |
Correlation Coefficient, Proper Motion in RA/RA |
|
|
ra_pmdec_corr |
pmdera |
Correlation Coefficient, Proper Motion in Dec/RA |
|
|
dec_parallax_corr |
plxde |
Correlation Coefficient, Parallax/Dec |
|
|
dec_pmra_corr |
pmrade |
Correlation Coefficient, Proper Motion in RA/RA |
|
|
dec_pmdec_corr |
pmdede |
Correlation Coefficient, Proper Motion in Dec/Dec |
|
|
parallax_pmra_corr |
pmraplx |
Correlation Coefficient, Proper Motion in RA/Parallax |
|
|
parallax_pmdec_corr |
pmdeplx |
Correlation Coefficient, Proper Motion in Dec/Parallax |
|
|
pmra_pmdec_corr |
pmdepmra |
Correlation Coefficient, Proper Motion in Dec/Proper Motion in RA |
|
Gaia Collaboration queries
This page contains many useful ADQL queries extracted from the DPAC documentation, including DPAC articles.
Content:
- Gaia FPR selected queries
- Gaia (E)DR3 selected queries
- Gaia DR2 selected queries
- Gaia DR1 selected queries
Gaia FPR selected queries
UPDATED ASTROMETRY FOR SOLAR SYSTEM OBJECTS
The following queries can be found in the Appendix section of the article: "Gaia Focused Product Release: Asteroid orbital solution" (Gaia Collaboration, P. David , et al. 2023):
Use case: I want to retrieve the state vector and semi-major axis uncertainty for all the valid orbital solutions, also excluding objects for which the heliocentric orbit cannot be computed (natural planetary satellites).
Notes: Note the filter for the first element of the covariance matrix, which turns out to be sometimes negative when the orbit solution is poor.
Target tables: gaiafpr.sso_source
Query:
SELECT number_mp, denomination, epoch_state_vector, ESDC_ARRAY_ELEMENT(h_state_vector,1) AS x, ESDC_ARRAY_ELEMENT(h_state_vector,2) AS y, ESDC_ARRAY_ELEMENT(h_state_vector,3) AS z, ESDC_ARRAY_ELEMENT(h_state_vector,4) AS vx,ESDC_ARRAY_ELEMENT(h_state_vector,5) AS vy, ESDC_ARRAY_ELEMENT(h_state_vector,6) AS vz, SQRT(ESDC_ARRAY_ELEMENT(orbital_elements_var_covar_matrix,1)) AS sigma_a FROM gaiafpr.sso_source WHERE ESDC_ARRAY_ELEMENT(orbital_elements_var_covar_matrix,1) > 0. ORDER BY number_mp ASC
Use case: I want to retrieve all the astrometric measurements for a given object based on its identifier.
Notes:
Target tables: gaiafpr.sso_observation
Query:
SELECT * FROM gaiafpr.sso_observation WHERE number_mp=704
Use case: I want to retrieve the astrometry for all asteroids associated to the best valid orbits with σa <1 x 10−10 au
Notes:
Target tables: gaiafpr.sso_source, gaiafpr.sso_observation
Query:
SELECT astrom.* FROM gaiafpr.sso_observation AS astrom INNER JOIN gaiafpr.sso_source AS so USING(number_mp) WHERE ESDC_ARRAY_ELEMENT(so.orbital_elements_var_covar_matrix,1) > 0. AND SQRT(ESDC_ARRAY_ELEMENT (so.orbital_elements_var_covar_matrix,1)) < 1.e-10 AND astrom.is_rejected = 'false'
Use case: I want to compute the time span covered by the observations of each asteroid
Notes:
Target tables: gaiafpr.sso_source, gaiafpr.sso_observation
Query:
SELECT number_mp, MAX(epoch) - MIN(epoch) AS t_delta_days FROM ( SELECT astrom.number_mp, astrom.epoch FROM gaiafpr.sso_observation AS astrom INNER JOIN gaiafpr.sso_source AS so USING(number_mp)) AS subquery WHERE(number_mp > 0) GROUP BY number_mp
DIFFUSE INTERSTELLAR BANDS FROM AGGREGATED RVS SPECTRA
See, for reference, the article: "Gaia Focused Product Release: Spatial distribution of two diffuse interstellar bands" (Gaia Collaboration, M. Schultheis , et al., 2023)
Use case: I want to retrieve the (stacked) interestellar medium spectra contained in a given region of the sky.
Notes:
Target tables: gaiafpr.interstellar_medium_spectra
Query:
SELECT * FROM gaiafpr.interstellar_medium_spectra AS gaia WHERE (gaia.lc > 10.0 AND gaia.lc < 15.0 AND gaia.bc > 2.0 AND gaia.bc < 6.0)
Use case: I want to retrieve the (stacked) interestellar medium spectra associated to the line of sight of a given source.
Notes: The GAIA_HEALPIX_INDEX UDF extracts the HEALPix level of order "norder" that is encoded in the gaia_source field.
Target tables: gaiafpr.interstellar_medium_spectra
Query:
SELECT * FROM gaiafpr.interstellar_medium_spectra WHERE healpix = GAIA_HEALPIX_INDEX(5, 5997091358307172224)
Use case: I want to retrieve the DIB parameters derived from the interestellar medium spectra associated to the line of sight of a given source.
Notes: The GAIA_HEALPIX_INDEX UDF extracts the HEALPix level of order "norder" that is encoded in the gaia_source field.
Target tables: gaiafpr.interstellar_medium_spectra
Query:
SELECT * FROM gaiafpr.interstellar_medium_params WHERE healpix = GAIA_HEALPIX_INDEX(5, 5997091358307172224)
ASTROMETRY AND PHOTOMETRY FROM ENGINEERING IMAGES TAKEN IN THE OMEGA CENTAURI REGION
See, for reference, the article: "Gaia Focused Product Release: Sources from Service Interface Function image analysis - half a million new sources in omega Centauri" (Gaia Collaboration, K. Weingrill, et al., 2023)
Use case: I want to retrieve all the Gaia SIF CF and Gaia DR3 sources within 0.8 degree radius around Omega centauri (ω Cen) cluster centre.
Notes: The field "n_scans" does not exist in "gaiadr3.gaia_source", so a value of -1 is used in the query in order to combine the output of the two queries. See this tutorial to learn more about the ADQL UNION operator.
Target tables: gaiafpr.crowded_field_source, gaiadr3.gaia_source
Query:
SELECT source_id, designation, ref_epoch, ra, ra_error, dec, dec_error, pmra, pmra_error, pmdec, pmdec_error, phot_g_mean_mag, l, b, n_scans FROM gaiafpr.crowded_field_source UNION SELECT source_id, designation, ref_epoch, ra, ra_error, dec, dec_error, pmra, pmra_error, pmdec, pmdec_error, phot_g_mean_mag, l, b, -1 AS nscans FROM gaiadr3.gaia_source WHERE DISTANCE(POINT(201.69399972775088, -47.484610741298994), POINT(ra, dec)) <0.8
EXTENDED RADIAL VELOCITY EPOCH DATA FOR LONG PERIOD VARIABLES
The following queries can be found in the Appendix D of the article: "Gaia Focused Product Release: Radial velocity time series of long-period variables" (Gaia Collaboration, M. Trabucchi, et al., 2023)
Use case: I want to retrieve selected quantities from the source catalog and LPV FPR catalog for all LPV FPR sources.
Notes:
Target tables: gaiadr3.gaia_source, gaiafpr.vari_long_period_variable
Query:
SELECT gs.source_id,gs.ra, gs.dec, fprlpv.frequency_rv, fprlpv.frequency_rv_error,fprlpv.amplitude_rv, fprlpv.flag_rv FROM gaiadr3.gaia_source AS gs LEFT JOIN gaiafpr.vari_long_period_variable AS fprlpv ON gs.source_id = fprlpv.source_id WHERE fprlpv.source_id IS NOT NULL
Use case: I want to retrieve all data from the gaiadr3.gaia_source catalogue, the LPV FPR catalogue, the RV statistics table, and the tables of data on LPVs from DR3 for all sources published in the LPV FPR
Notes:
Target tables: gaiadr3.gaia_source, gaiafpr.vari_long_period_variable, gaiadr3.vari_long_period_variable, gaiadr3.vari_summary
Query:
SELECT * FROM gaiadr3.gaia_source AS src LEFT JOIN gaiafpr.vari_long_period_variable AS fprlpv USING (source_id) LEFT JOIN gaiafpr.vari_rad_vel_statistics AS rvstat USING (source_id) LEFT JOIN gaiadr3.vari_long_period_variable AS lpv USING (source_id) LEFT JOIN gaiadr3.vari_summary AS varistat USING (source_id) WHERE fprlpv.source_id IS NOT NULL
Use case: I want to retrieve all the RV time series published as part of this FPR using a source.
Notes:
Target tables: gaiafpr.interstellar_medium_spectra
Query:
SELECT fprlpv.source_id, varirv.transit_id,varirv.rv_obs_time,varirv.radial_velocity,varirv.radial_velocity_error, varirv.rejected_by_variability FROM gaiafpr.vari_long_period_variable AS fprlpv LEFT JOIN gaiafpr.vari_epoch_radial_velocity AS varirv USING (source_id) WHERE fprlpv.source_id IS NOT NULL
Gaia (E)DR3 selected queries
Integrated extragalactic tables
The integrated extragalactic tables (see Chapter 12 in the Gaia DR3 documentation) are composed of sources stemming from various DPAC processing modules, with overlaps between the corrresponding sub-samples. We indicate here how these can be selected based on ADQL queries on the qso_candidates and galaxy_candidates tables.
DSC and DSC-joint samples
The DSC sources used in the samples described in this chapter can be obtained with the following queries in the respective qso_candidates and galaxy_candidates tables:
SELECT source_id FROM gaiadr3.qso_candidates WHERE MOD(source_selection_flags,POWER(2,6+1))-MOD(source_selection_flags,POWER(2,6)) != 0
SELECT source_id FROM gaiadr3.galaxy_candidates WHERE MOD(source_selection_flags,POWER(2,3+1))-MOD(source_selection_flags,POWER(2,3)) != 0
Similarly, the following provides the sources from the DSC-Joint samples of quasars and galaxies:
SELECT source_id FROM gaiadr3.qso_candidates WHERE classlabel_dsc_joint = 'quasar'
SELECT source_id FROM gaiadr3.galaxy_candidates WHERE classlabel_dsc_joint = 'galaxy'
Vari-Classification samples
The respective 'AGN' and 'GALAXY' samples from the Vari-Classification module are selected as follows:
SELECT source_id FROM gaiadr3.qso_candidates WHERE vari_best_class_name = 'AGN'
SELECT source_id FROM gaiadr3.galaxy_candidates WHERE vari_best_class_name = 'GALAXY'
Vari-AGN sample
The Vari-AGN sample is simply obtained by:
SELECT source_id FROM gaiadr3.qso_candidates WHERE qso_variability IS NOT NULL
Surface brightness samples
The sources considered eligible from the surface brightness samples are selected as:
SELECT source_id FROM gaiadr3.qso_candidates WHERE host_galaxy_flag < 6
SELECT source_id FROM gaiadr3.galaxy_candidates WHERE radius_sersic IS NOT NULL
Quasar classifier (SOC) sample
The sources considered eligible from the QSOC processing (see Chapter 11.3.14 in the Gaia DR3 documentation) are selected as:
SELECT source_id FROM gaiadr3.qso_candidates WHERE source_selection_flags >= 128
The following query shows how to select quasar candidates having the kth bit of the flags_qsoc set to a certain value:
SELECT * FROM gaiadr3.qso_candidates WHERE MOD(flags_qsoc,POWER(2,k+1)) - MOD(flags_qsoc,POWER(2,k)) <> 0
And the query below shows how to select quasar candidates having both an estimated redshift from QSOC and XP continuous spectra available via DataLink.
SELECT gdr3.source_id, gdr3.ra, gdr3.dec, gdr3.phot_g_mean_mag, gdr3.phot_bp_mean_mag, gdr3.phot_rp_mean_mag, qso.redshift_qsoc, qso.flags_qsoc FROM gaiadr3.qso_candidates AS qso JOIN gaiadr3.gaia_source AS gdr3 USING (source_id) WHERE qso.redshift_qsoc IS NOT NULL AND gdr3.has_xp_continuous = 'TRUE'
Unresolved Galaxy Classifier (UGC) sample
The sources considered eligible from the UGC (see Chapter 11.3.13 in the Gaia DR3 documentation) processing are selected as:
SELECT source_id FROM gaiadr3.galaxy_candidates WHERE redshift_ugc IS NOT NULL
The total number of galaxy candidates having estimated redshifts by UGC can be computed as follows:
SELECT COUNT(*) FROM gaiadr3.galaxy_candidates WHERE redshift_ugc IS NOT NULL
OA samples
Although not used to define which sources should enter into the integrated extragalactic tables, the OA sources used in this chapter can be obtained by simply selecting those sources where field classlabel_oa is not null.
Astrophysical parameters tables
This section contains different use cases mostly related to the astrophysical_parameters and astrophysical_parameters_supp tables. The examples are sorted following the structure of Sect 11.3 (Apsis modules) in the Gaia DR3 documentation.
Chapter 11.3.2: Discrete Source classifier (DSC)
Use case: Select high-probability quasars according to their Specmod and Allosmod probabilities, excluding circular regions centred in the Large and Small Magallanic Clouds with radii of 9 and 6 degrees, respectively.
Notes: The "<>" operator stands for "not equal to" in PostgreSQL
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.gaia_source_lite
Query:
SELECT gaia.source_id FROM gaiadr3.astrophysical_parameters JOIN gaiadr3.gaia_source_lite AS gaia USING (source_id) WHERE gaia.in_qso_candidates = 'true' AND classprob_dsc_specmod_quasar > 0.9 AND classprob_dsc_allosmod_quasar > 0.9 AND 1 <> CONTAINS(POINT(81.3, -68.7), CIRCLE(gaia.ra, gaia.dec, 9.0)) AND 1 <> CONTAINS(POINT(16.0, -72.8), CIRCLE(gaia.ra, gaia.dec, 6.0))
Chapter 11.3.3: General Stellar Parametrizer from Photometry (GSP-Phot)
Use case: Select a random sample of best measured giant stars having A0 < 1 mag within a distance < 5 kpc.
Notes:
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.gaia_source_lite
Query:
SELECT gaia.source_id, gaia.l, gaia.b, gaia.phot_g_mean_mag, apsis.teff_gspphot, apsis.logg_gspphot, apsis.mh_gspphot, apsis.azero_gspphot, apsis.distance_gspphot, apsis.distance_gspphot_lower, apsis.distance_gspphot_upper, apsis.libname_gspphot FROM gaiadr3.astrophysical_parameters AS apsis JOIN gaiadr3.gaia_source_lite AS gaia USING (source_id) WHERE apsis.azero_gspphot < 1 AND apsis.distance_gspphot < 5000 AND apsis.logg_gspphot BETWEEN 0 AND 3 AND gaia.random_index < 100000
Chapter 11.3.4: General Stellar Parametrizer from Spectroscopy (GSP-Spec)
Use case: Select the atmospheric parameters for a high-quality sample (first 13 GSP-Spec parameter flags equal to zero) of 10,000 stars (see flags_gspspec for details).
Notes:
Target tables: gaiadr3.astrophysical_parameters
Query:
SELECT TOP 10000 source_id, flags_gspspec, teff_gspspec, logg_gspspec, mh_gspspec, alphafe_gspspec FROM gaiadr3.astrophysical_parameters WHERE flags_gspspec LIKE '0000000000000%'
Use case: Return Teff, log g, and [Fe/H] (not [M/H]) and [Ca/Fe] (computing their uncertainties), for a sample of 10,000 stars using a selection criterion based on the Fe and Ca GSP-Spec flags equal to 0. The KMgiantPar flag is allowed to be 0 or 1 (see flags_gspspec description for details).
Notes:
Target tables: gaiadr3.astrophysical_parameters
Query:
WITH gsp_ap AS ( SELECT source_id, flags_gspspec, teff_gspspec, logg_gspspec, mh_gspspec + fem_gspspec AS feh_gspspec, cafe_gspspec, 0.5*SQRT(POWER(mh_gspspec_upper-mh_gspspec_lower, 2) + POWER(fem_gspspec_upper-fem_gspspec_lower, 2)) AS feh_gspspec_sigma, 0.5*(cafe_gspspec_upper-cafe_gspspec_lower) AS cafe_gspspec_sigma, spectraltype_esphs FROM gaiadr3.astrophysical_parameters) SELECT TOP 10000 source_id, feh_gspspec, feh_gspspec_sigma, cafe_gspspec, cafe_gspspec_sigma, teff_gspspec, spectraltype_esphs, logg_gspspec, flags_gspspec FROM gsp_ap WHERE (flags_gspspec LIKE '0000000000000________00____00%' OR flags_gspspec LIKE '0000000000001________00____00%') AND feh_gspspec_sigma < 0.1 AND cafe_gspspec_sigma < 0.1
Use case: Retrieve Artificial Neural Network (ANN) parametrisation results for high-quality objects (see flags_gspspec description for details).
Notes: As an alternative (that produces identical output and has similar execution time), the WHERE clause could be modified as: ... WHERE flags_gspspec_ann LIKE '000000000000'
Target tables: astrophysical_parameters_supp
Query:
SELECT source_id, teff_gspspec_ann, teff_gspspec_ann_lower, teff_gspspec_ann_upper, logg_gspspec_ann, logg_gspspec_ann_lower, logg_gspspec_ann_upper, mh_gspspec_ann, mh_gspspec_ann_lower, mh_gspspec_ann_upper, alphafe_gspspec_ann, alphafe_gspspec_ann_lower, alphafe_gspspec_ann_upper, logchisq_gspspec_ann, flags_gspspec_ann FROM astrophysical_parameters_supp WHERE CAST(flags_gspspec_ann AS BIGINT) = 0
Use case: Retrieve the first 1,000 high-quality objects with all necessary parameters from ANN to plot Kiel, [alpha/Fe] versus [M/H], log g versus [M/H], and Teff versus G diagrams (see flags_gspspec description for details).
Notes:
Target tables: gaiadr3.astrophysical_parameters_supp, gaiadr3.gaia_source_lite
Query:
SELECT TOP 1000 gs.source_id, aps.teff_gspspec_ann AS teff, aps.logg_gspspec_ann AS logg, aps.mh_gspspec_ann AS mh, aps.alphafe_gspspec_ann AS alphafe, gs.phot_g_mean_mag + 5.0 * log10(gs.parallax) + 10.0 AS abs_gmag FROM gaiadr3.gaia_source_lite AS gs RIGHT JOIN gaiadr3.astrophysical_parameters_supp AS aps USING (source_id) WHERE gs.parallax > 0 AND CAST(aps.flags_gspspec_ann AS BIGINT) = 0)
Chapter 11.3.5: Multiple Star Classifier (MSC)
Use case: Select distances from MSC and GSP-Phot for a random subset of sources with parallax SNR > 10.
Notes:
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.gaia_source_lite
Query:
SELECT gaia.source_id, gaia.parallax, gaia.parallax_error, apsis.distance_gspphot, apsis.distance_msc, apsis.teff_msc1, apsis.teff_msc2, apsis.flags_msc FROM gaiadr3.gaia_source_lite AS gaia JOIN gaiadr3.astrophysical_parameters AS apsis USING (source_id) WHERE gaia.random_index < 100000 AND gaia.parallax_over_error > 10 AND apsis.distance_gspphot IS NOT NULL AND apsis.distance_msc IS NOT NULL
Chapter 11.3.6: Final Luminosity Age Mass Estimator (FLAME)
Use case: To derive the distributions of FLAME parameters and uncertainties for about five thousand stars randomly chosen.
Notes:
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.gaia_source_lite
Query:
SELECT ap.source_id, ap.age_flame, ap.age_flame_lower, ap.age_flame_upper, ap.mass_flame, ap.mass_flame_lower, ap.mass_flame_upper, ap.lum_flame, ap.lum_flame_lower, ap.lum_flame_upper, ap.radius_flame, ap.radius_flame_lower, ap.radius_flame_upper, ap.gravredshift_flame, ap.gravredshift_flame_lower, ap.gravredshift_flame_upper, ap.evolstage_flame, ap.flags_flame, ap.bc_flame, ap.teff_gspphot, ap.mh_gspphot, ap.logg_gspphot, ap.ag_gspphot, ap.radius_gspphot, ap.distance_gspphot, ap.mg_gspphot, gs.parallax, gs.parallax_error, gs.phot_g_mean_mag, gs.phot_bp_mean_mag, gs.phot_rp_mean_mag, gs.l, gs.b, gs.ra, gs.dec, gs.pmra, gs.pmdec FROM gaiadr3.astrophysical_parameters AS ap JOIN gaiadr3.gaia_source_lite AS gs USING(source_id) WHERE ap.lum_flame IS NOT NULL AND ap.bc_flame IS NOT NULL AND random_index < 32500
Use case: Select a sample of sources that use the parallax instead of the distance (better sample) and get their masses (see the flags_flame description for details).
Notes:
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.gaia_source
Query:
SELECT mass_flame, source_id FROM gaiadr3.astrophysical_parameters WHERE flags_flame = '20' OR flags_flame = '10' OR flags_flame = '00'
Chapter 11.3.7: Extended Stellar Parametrizer for Emission-Line Stars (ESP-ELS)
Use case: Get the Halpha pseudo-equivalenth width information for 1,000 random candidate Be stars with Halpha < -2 nm and class label quality better than 3 (see the classlabel_espels_flag description for details).
Notes:
Target tables: gaiadr3.astrophysical_parameters
Query:
SELECT TOP 1000 ap.source_id, ap.ew_espels_halpha, ap.ew_espels_halpha_uncertainty, ap.ew_espels_halpha_model, ap.ew_espels_halpha_flag FROM gaiadr3.astrophysical_parameters AS ap WHERE ap.classlabel_espels = 'beStar' AND ap.ew_espels_halpha < -2 AND CAST(ap.classlabel_espels_flag AS INTEGER) <= 2
Chapter 11.3.8: Extended Stellar Parametrizer for Hot Stars (ESP-HS)
Use case: Select the first 1,000 results from the ESP-HS module in RVS+XP mode (see the flags_esphs description for details).
Notes:
Target tables: gaiadr3.astrophysical_parameters
Query:
SELECT TOP 1000 source_id, teff_esphs, teff_esphs_uncertainty, logg_esphs, logg_esphs_uncertainty, vsini_esphs, vsini_esphs_uncertainty, ag_esphs, ag_esphs_uncertainty, azero_esphs, azero_esphs_uncertainty, ebpminrp_esphs, ebpminrp_esphs_uncertainty, flags_esphs FROM gaiadr3.astrophysical_parameters WHERE teff_esphs > 0 AND CAST(flags_esphs AS INTEGER) < 10
Use case: Select the first 1,000 results from the ESP-HS module in XP-only mode (see the flags_esphs description for details).
Notes:
Target tables: gaiadr3.astrophysical_parameters
Query:
SELECT TOP 1000 source_id, teff_esphs, teff_esphs_uncertainty, logg_esphs, logg_esphs_uncertainty, ag_esphs, ag_esphs_uncertainty, azero_esphs, azero_esphs_uncertainty, ebpminrp_esphs, ebpminrp_esphs_uncertainty, flags_esphs FROM gaiadr3.astrophysical_parameters WHERE teff_esphs > 0 AND CAST(flags_esphs AS INTEGER) > 10
Chapter 11.3.12: Outlier Analysis (OA)
Use case: Retrieve all the sources that belong to a certain neuron. In this example, the first neuron (located at (0,0), and identified by neuron_id = 202105281205440000) is used.
Notes:
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.oa_neuron_information
Query:
SELECT ap.source_id FROM gaiadr3.oa_neuron_information AS neuron JOIN gaiadr3.astrophysical_parameters AS ap ON neuron.neuron_id = ap.neuron_oa_id WHERE neuron.neuron_id = 202105281205440000
Use case: Obtain the statistical parameters that were computed for the neuron where a given source lies in.
Notes:
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.oa_neuron_information
Query:
SELECT neuron.* FROM gaiadr3.astrophysical_parameters AS ap JOIN gaiadr3.oa_neuron_information AS neuron ON ap.neuron_oa_id = neuron.neuron_id WHERE ap.source_id = 4296182638654046592
Use case: Retrieve the first 100 sources that belong to a SOM neuron that were assigned a specific class label. For this example, all galaxy labels are considered.
Notes:
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.oa_neuron_information
Query:
SELECT TOP 100 ap.source_id, neuron.* FROM gaiadr3.oa_neuron_information AS neuron JOIN gaiadr3.astrophysical_parameters AS ap ON neuron.neuron_id = ap.neuron_oa_id WHERE neuron.class_label LIKE 'GAL%'
Use case: Obtain all the neurons that achieve a certain quality category threshold. In this example, just high-quality neurons (HQN) are retrieved.
Notes:
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.oa_neuron_information
Query:
SELECT * FROM gaiadr3.oa_neuron_information WHERE quality_category < 4
Use case: Identify the best-quality sources that are assigned to a certain neuron by applying a filter on the distance between the source XP spectra and the neuron prototype. In this example, the first neuron (located at (0,0), and identified by neuron_id = 202105281205440000) is used, as well as a distance filter based on the neuron_oa_dist_percentile_rank field.
Notes: Defining a filter based on the neuron_oa_dist field from the astrophysical_parameters table could provide a much finer filtering.
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.oa_neuron_information
Query:
SELECT ap.source_id FROM gaiadr3.oa_neuron_information AS neuron JOIN gaiadr3.astrophysical_parameters AS ap ON neuron.neuron_id = ap.neuron_oa_id WHERE neuron.neuron_id = 202105281205440000 AND ap.neuron_oa_dist_percentile_rank >= 75
Use case: Identify the first 100 best quality sources that are assigned to any neuron by applying a filter based on both the neuron quality index and the distance between the source XP spectra and the neuron prototype.
Notes:
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.oa_neuron_information
Query:
SELECT TOP 100 ap.source_id FROM gaiadr3.oa_neuron_information AS neuron JOIN gaiadr3.astrophysical_parameters AS ap ON neuron.neuron_id = ap.neuron_oa_id WHERE neuron.quality_category < 4 AND ap.neuron_oa_dist < 0.001
Use case: Given a certain source, retrieve the XP spectrum of the neuron prototype that represents such a source. Note that the outputs should be ordered by the prototype wavelength in order to be able to reconstruct the XP spectrum.
Notes:
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.oa_neuron_xp_spectra
Query:
SELECT spectra.xp_spectrum_prototype_wavelength, spectra.xp_spectrum_prototype_flux FROM gaiadr3.astrophysical_parameters AS ap JOIN gaiadr3.oa_neuron_xp_spectra AS spectra ON ap.neuron_oa_id = spectra.neuron_id WHERE ap.source_id = 4296182638654046592 ORDER BY spectra.xp_spectrum_prototype_wavelength
Chapter 11.3.13: Unresolved Galaxy Classifier (UGC)
Use case: Count galaxy candidates having estimated redshifts by UGC.
Notes:
Target tables: gaiadr3.galaxy_candidates
Query:
SELECT COUNT(*) FROM gaiadr3.galaxy_candidates WHERE redshift_ugc IS NOT NULL
Use case: Retrieve the UGC parameters for 10 galaxy candidates having estimated redshift.
Notes:
Target tables: gaiadr3.galaxy_candidates
Query:
SELECT TOP 10 source_id, redshift_ugc, redshift_ugc_upper, redshift_ugc_lower FROM gaiadr3.galaxy_candidates WHERE redshift_ugc IS NOT NULL
Chapter 11.3.14: Quasar Classifier (QSOC)
Use case: Select quasar candidates having the kth bit of the flags_qsoc set to a certain value.
Target tables: gaiadr3.qso_candidates
Query:
SELECT * FROM gaiadr3.qso_candidates WHERE MOD(flags_qsoc,POWER(2,k+1)) - MOD(flags_qsoc,POWER(2,k)) <> 0
Use case: Select quasar candidates having both an estimated redshift from QSOC and XP continuous spectra available via DataLink.
Notes:
Target tables: gaiadr3.astrophysical_parameters, gaiadr3.gaia_source
Query:
SELECT gdr3.source_id, gdr3.ra, gdr3.dec, gdr3.phot_g_mean_mag, gdr3.phot_bp_mean_mag, gdr3.phot_rp_mean_mag, qso.redshift_qsoc, qso.flags_qsoc FROM gaiadr3.qso_candidates AS qso JOIN gaiadr3.gaia_source AS gdr3 USING (source_id) WHERE qso.redshift_qsoc IS NOT NULL AND gdr3.has_xp_continuous = 'TRUE'
The celestial reference frame (Gaia-CRF3)
Use case: I want to retrieve the astrometric data for all the 1,614,173 Gaia-CRF3 sources (Gaia Early Data Release 3: The celestial reference frame (Gaia-CRF3)).
Target tables: gaiaedr3.gaia_source, gaiaedr3.agn_cross_id
Query:
SELECT agn.source_name_in_catalogue, agn.catalogue_name, edr3.* FROM gaiaedr3.agn_cross_id AS agn INNER JOIN gaiaedr3.gaia_source AS edr3 USING (source_id)
Gaia-CRF3: 5 parameter solutions
Use case: I want to retrieve the astrometric data for the Gaia-CRF3 sources with five-parameter astrometric solutions (Gaia Early Data Release 3: The celestial reference frame (Gaia-CRF3)).
Notes: Replacing '31' by '95' one gets the data for the 398,231 sources with six-parameter solutions.
Target tables: gaiaedr3.gaia_source, gaiaedr3.agn_cross_id
Query:
SELECT agn.source_name_in_catalogue, agn.catalogue_name, edr3.* FROM gaiaedr3.agn_cross_id AS agn INNER JOIN gaiaedr3.gaia_source AS edr3 USING (source_id) WHERE edr3.astrometric_params_solved = 31
gaia-crf3: ORIENTATION sources
Use case: I want to retrieve the data for the 2007 sources that were used to fix the orientation of Gaia-CRF3 (Gaia Early Data Release 3: The celestial reference frame (Gaia-CRF3)).
Notes: The complexity of the query results from the fact that gaiaedr3.frame_rotator_source can contain sources that are NOT in gaiaedr3.agn_cross_id.
Target tables: gaiaedr3.gaia_source, gaiaedr3.agn_cross_id
Query:
SELECT sub.source_name_in_catalogue, sub.catalogue_name, edr3.* FROM ( SELECT frame.source_id, agn.source_name_in_catalogue, agn.catalogue_name FROM gaiaedr3.frame_rotator_source AS frame LEFT OUTER JOIN gaiaedr3.agn_cross_id AS agn USING (source_id) WHERE frame.used_for_reference_frame_orientation = 'True' ) AS sub INNER JOIN gaiaedr3.gaia_source AS edr3 USING (source_id)
gaia-crf3: SPIN sources
Use case: I want to retrieve the data for the 428,034 sources used to define the rotation (spin) of Gaia-CRF3 (Gaia Early Data Release 3: The celestial reference frame (Gaia-CRF3)).
Notes: The complexity of the query results from the fact that gaiaedr3.frame_rotator_source can contain sources that are NOT in gaiaedr3.agn_cross_id.
Target tables: gaiaedr3.gaia_source, gaiaedr3.agn_cross_id
Query:
SELECT sub.source_name_in_catalogue, sub.catalogue_name, edr3.* FROM ( SELECT frame.source_id, agn.source_name_in_catalogue, agn.catalogue_name FROM gaiaedr3.frame_rotator_source AS frame LEFT OUTER JOIN gaiaedr3.agn_cross_id AS agn USING (source_id) WHERE frame.used_for_reference_frame_spin = 'True' ) AS sub INNER JOIN gaiaedr3.gaia_source AS edr3 USING (source_id)
gaia crf3: catalogue selection
Use case: I want to retrieve the Gaia-CRF3 sources from a given external catalog: "$$$" should be replaced by the catalogue code given in Table 1 in Gaia Early Data Release 3: The celestial reference frame (Gaia-CRF3).
Notes: This query involves EDR3 and DR3 tables.
Target tables: gaiaedr3.gaia_source, gaiaedr3.agn_cross_id
Query:
SELECT xm.$$$_name, edr3.* FROM gaiadr3.gaia_source AS edr3 INNER JOIN gaiadr3.gaia_crf3_xm AS xm USING (source_id) WHERE xm.$$$ = 'True'
gaia crf3: confusion sources
Use case: I want to retrieve the data for the 30,723,995 confusion sources in GEDR3 with five-parameter solutions (adapted from Gaia Early Data Release 3: The celestial reference frame (Gaia-CRF3)).
Notes: Replacing '31' by '95' gives the 182,814,959 confusion sources with six-parameter solutions. This query is somewhat dangerous since taken verbatim it returns huge tables.
Target tables: gaiaedr3.gaia_source, gaiaedr3.agn_cross_id
Query:
SELECT * FROM gaiaedr3.gaia_source AS g WHERE g.astrometric_params_solved = 31 AND ABS((g.parallax + 0.017)/g.parallax_error) < 5 AND ( POWER(g.pmra/g.pmra_error,2) + POWER(g.pmdec/g.pmdec_error,2) -2*g.pmra_pmdec_corr*g.pmra/g.pmra_error*g.pmdec/g.pmdec_error)/ (1-POWER(g.pmra_pmdec_corr,2)) < 25
Synthetic photometry from Gaia XP spectra - PVP
Use case: I want to retrieve SDSS synthetic photometery for the sources that have an absolute corrected BP/RP flux excess factor smaller than the 1-sigma relation suggested in Gaia Early Data Release 3: Photometric content and validation.
Notes: This query runs on a 0.001 random selection of the Gaia source catalogue thanks to the additional constraint on random_index.
Target tables: gaiadr3.gaia_source, gaiadr3.synthetic_photometry_gspc
Query:
SELECT dr3.source_id, dr3.ra, dr3.dec, dr3.parallax, dr3.parallax_over_error, dr3.ruwe, gspc.g_sdss_mag, gspc.i_sdss_mag FROM gaiadr3.gaia_source AS dr3 INNER JOIN gaiadr3.synthetic_photometry_gspc AS gspc USING (source_id) WHERE ABS(gspc.c_star)<(0.0059898 + 8.817481e-12 * POWER(dr3.phot_g_mean_mag, 7.618399)) AND dr3.random_index < 1811709
Synthetic photometry from Gaia XP spectra - PVP (II)
Use case: I want to retrieve some selected parameters from the main Gaia DR3 table and all the parameters available in the GSPC for a given set of stars, i.e. those having |b|> 50 deg (Galactic Caps). Selections in RUWE and in c_star (following the criterion suggested by Gaia Early Data Release 3: Photometric content and validation) are also adopted.
Target tables: gaiadr3.gaia_source_lite, gaiadr3.synthetic_photometry_gspc
Notes: Execution time ~25 mins. Job output size = 1.3 GB.
Query:
SELECT dr3.source_id, dr3.ra, dr3.dec, dr3.parallax, dr3.parallax_error, dr3.pmra, dr3.pmra_error, dr3.pmdec, dr3.pmdec_error, dr3.phot_g_mean_mag, dr3.phot_bp_mean_mag, dr3.phot_rp_mean_mag, dr3.bp_rp, dr3.radial_velocity, dr3.radial_velocity_error, dr3.ruwe, dr3.phot_variable_flag, dr3.non_single_star, dr3.teff_gspphot, dr3.logg_gspphot, dr3.mh_gspphot, dr3.distance_gspphot, dr3.ag_gspphot, gspc.c_star, gspc.u_sdss_mag, gspc.g_sdss_mag,gspc.r_sdss_mag, gspc.i_sdss_mag, gspc.z_sdss_mag, gspc.u_jkc_mag, gspc.b_jkc_mag,gspc.v_jkc_mag, gspc.r_jkc_mag, gspc.i_jkc_mag, gspc.y_ps1_mag, f606w_acswfc_mag, f814w_acswfc_mag, 1.086*(gspc.u_sdss_flux_error/gspc.u_sdss_flux) AS du_sdss, 1.086*(gspc.g_sdss_flux_error/gspc.g_sdss_flux) AS dg_sdss, 1.086*(gspc.r_sdss_flux_error/gspc.r_sdss_flux) AS dr_sdss, 1.086*(gspc.i_sdss_flux_error/gspc.i_sdss_flux) AS di_sdss, 1.086*(gspc.z_sdss_flux_error/gspc.z_sdss_flux) AS dz_sdss, 1.086*(gspc.u_jkc_flux_error/gspc.u_jkc_flux) AS du_jkc, 1.086*(gspc.b_jkc_flux_error/gspc.b_jkc_flux) AS db_jkc, 1.086*(gspc.v_jkc_flux_error/gspc.v_jkc_flux) AS dv_jkc, 1.086*(gspc.r_jkc_flux_error/gspc.r_jkc_flux) AS dr_jkc, 1.086*(gspc.i_jkc_flux_error/gspc.i_jkc_flux) AS di_jkc, 1.086*(gspc.y_ps1_flux_error/gspc.y_ps1_flux) AS dy_ps1, 1.086*(gspc.f606w_acswfc_flux_error/gspc.f606w_acswfc_flux) AS df606w_acswfc, 1.086*(gspc.f814w_acswfc_flux_error/gspc.f814w_acswfc_flux) AS df814w_acswfc, gspc.u_sdss_flag, gspc.g_sdss_flag, gspc.r_sdss_flag, gspc.i_sdss_flag, gspc.z_sdss_flag, gspc.u_jkc_flag, gspc.b_jkc_flag, gspc.v_jkc_flag, gspc.r_jkc_flag, gspc.i_jkc_flag, gspc.y_ps1_flag, gspc.f606w_acswfc_flag, gspc.f606w_acswfc_flag FROM gaiadr3.gaia_source_lite AS dr3 INNER JOIN gaiadr3.synthetic_photometry_gspc AS gspc USING (source_id) WHERE ABS(dr3.b)>50.0 AND dr3.ruwe<1.3 AND ABS(gspc.c_star)<(0.0059898 + 8.817481e-12 * POWER(dr3.phot_g_mean_mag,7.618399))
Extragalactic objects in Gaia DR3 (QSOS PURER SUBSET)
Use case: Selects the purer subset of quasars recommended by Gaia Data Release 3: The extragalactic content.
Target table: gaiadr3.qso_candidates
Query:
SELECT * FROM gaiadr3.qso_candidates WHERE (gaia_crf_source = 'True' OR host_galaxy_flag<6 OR classlabel_dsc_joint = 'quasar' OR vari_best_class_name = 'AGN')
Extragalactic objects in Gaia DR3 (GALAXIES PURER SUBSET)
Use case: Selects the purer subset of galaxies recommended by Gaia Data Release 3: The extragalactic content.
Target table: gaiadr3.galaxy_candidates
Query:
SELECT * FROM gaiadr3.galaxy_candidates WHERE (radius_sersic IS NOT NULL OR classlabel_dsc_joint = 'galaxy' OR vari_best_class_name = 'GALAXY')
Extragalactic objects in Gaia DR3
Use case: Shows how to combine three tables to select sources with higher classification probabilities that exclude the LMC and SMC (extracted from Gaia Data Release 3: The extragalactic content).
Target tables: gaiadr3.qso_candidates, gaiadr3.astrophysical_parameters
Query:
SELECT source_id FROM (SELECT * FROM gaiadr3.qso_candidates JOIN gaiadr3.astrophysical_parameters USING (source_id) WHERE classprob_dsc_specmod_quasar>0.9 AND classprob_dsc_allosmod_quasar>0.9 ) AS temp JOIN gaiadr3.gaia_source USING (source_id) WHERE 1 != CONTAINS( POINT(81.3, -68.7), CIRCLE(ra, dec, 9.0)) AND 1 != CONTAINS( POINT(16.0, -72.8), CIRCLE(ra, dec, 6.0))
Golden sample of Astrophysical Parameters
Use case: The query used iteratively for the analysis and selection of the FGKM sample of stars. The iteration runs over random_index in steps of 10,000,000 sources (Gaia Data Release 3: A golden sample of astrophysical parameters).
Target tables: gaiadr3.gaia_source, gaiadr3.astrophysical_parameters, gaiadr3.astrophysical_parameters_supp
Query:
SELECT gs.source_id, phot_bp_mean_mag, phot_rp_mean_mag, phot_bp_mean_flux_over_error, phot_rp_mean_flux_over_error, phot_g_mean_mag, parallax_error, parallax, parallax_over_error, astrometric_excess_noise, astrometric_excess_noise_sig, ruwe, ipd_gof_harmonic_amplitude, rvs_spec_sig_to_noise, rv_expected_sig_to_noise, ap.ebpminrp_gspphot, ap.radius_gspphot, ap.teff_gspphot, ap.logg_gspphot, ap.mg_gspphot, ap.abp_gspphot, gs.ag_gspphot, ap.arp_gspphot, ap.teff_gspphot_upper, gs.mh_gspphot, ap.teff_gspphot_lower, mg_gspphot_lower, mg_gspphot_upper, ap.ebpminrp_gspphot_lower,ap.ebpminrp_gspphot_upper, ap.ag_gspphot_upper, ap.ag_gspphot_lower, ap.mh_gspphot_upper, ap.mh_gspphot_lower, ap.logg_gspphot_upper, ap.logg_gspphot_lower, teff_gspphot_marcs, teff_gspphot_phoenix, logg_gspphot_marcs, logg_gspphot_phoenix, radius_flame, mass_flame, age_flame, evolstage_flame, lum_flame, bc_flame, radius_flame_upper, radius_flame_lower, lum_flame_upper, lum_flame_lower, mass_flame_upper, mass_flame_lower, age_flame_upper, age_flame_lower, flags_flame, spectraltype_esphs, flags_esphs, teff_gspspec, mh_gspspec, logg_gspspec, alphafe_gspspec, teff_gspspec_upper, teff_gspspec_lower, logg_gspspec_upper, logg_gspspec_lower, mh_gspspec_upper, mh_gspspec_lower, radius_flame_spec, lum_flame_spec, age_flame_spec, mass_flame_spec, evolstage_flame_spec, radius_flame_spec_upper, radius_flame_spec_lower, lum_flame_spec_lower, lum_flame_spec_upper, mass_flame_spec_upper, mass_flame_spec_lower, age_flame_spec_lower, age_flame_spec_upper, bc_flame_spec FROM gaiadr3.gaia_source AS gs INNER JOIN gaiadr3.astrophysical_parameters_supp AS aps USING (source_id) INNER JOIN gaiadr3.astrophysical_parameters AS ap USING (source_id) WHERE ipd_frac_multi_peak < 6 AND parallax_over_error >10 AND gs.teff_gspphot > 2500 AND gs.teff_gspphot < 7500 AND gs.distance_gspphot < 1e3/(parallax-4*parallax_error) AND gs.distance_gspphot > 1e3/(parallax +4*parallax_error) AND gs.libname_gspphot='MARCS' AND gs.classprob_dsc_combmod_star > 0.9 AND gs.mh_gspphot > -0.8 AND ABS(teff_gspphot_marcs - teff_gspphot_phoenix + 65) < 150 AND radius_gspphot < 100 and mg_gspphot < 12 AND random_index >= 1600000000 AND random_index < 1610000000
RETRIEVE SAMPLE OF OB STARS IN THE MILKY WAY SPIRAL ARMS
Use case: I want to retrieve the sample of OB stars used in the Mapping the spiral arms of the Milky Way (Gaia Data Release 3: Mapping the asymmetric disc of the Milky Way).
Target table: gaiadr3.gaia_source, gaiadr3.astrophysical_parameters
Query:
SELECT g.*, ap.* FROM gaiadr3.gaia_source AS g INNER JOIN gaiadr3.astrophysical_parameters AS ap ON g.source_id = ap.source_id WHERE ( (ap.teff_gspphot > 10000 AND (ap.spectraltype_esphs = 'O' OR ap.spectraltype_esphs = 'B' OR ap.spectraltype_esphs = 'A') AND ap.teff_esphs IS NULL) OR (ap.teff_esphs > 10000 AND ap.teff_gspphot > 8000) OR (ap.teff_esphs > 10000 AND ap.teff_esphs < 50000 AND ap.teff_gspphot IS NULL)) AND power(g.parallax/100.,5) < power(10.,2.-g.phot_g_mean_mag+1.8*g.bp_rp)
RETRIEVE SAMPLE OF RGB STARS IN THE MILKY WAY SPIRAL ARMS
Use case: I want to retrieve the sample of RGB stars used in the Mapping the spiral arms of the Milky Way (Gaia Data Release 3: Mapping the asymmetric disc of the Milky Way).
Target table: gaiadr3.gaia_source
Query:
SELECT g.* FROM gaiadr3.gaia_source AS g WHERE (g.teff_gspphot<5500 AND g.teff_gspphot>3000) AND (g.logg_gspphot<3.)
Chemical cartography of the Milky Way disc
Use case: I want to retrieve the "medium quality sample" of stars with GSPspec parameters described in (Gaia Data Release 3: Chemical cartography of the Milky Way - see their Sect. 2.5)
Target table: gaiadr3.astrophysical_parameters
Query:
SELECT source_id FROM gaiadr3.astrophysical_parameters WHERE (teff_gspspec>3500) AND (logg_gspspec>0) AND (logg_gspspec<5) AND ((teff_gspspec_upper-teff_gspspec_lower)<750) AND ((logg_gspspec_upper-logg_gspspec_lower)<1.) AND ((mh_gspspec_upper-mh_gspspec_lower)<.5) AND (teff_gspspec>=3800 OR logg_gspspec<=3.5) AND (teff_gspspec>=4150 OR logg_gspspec<=2.4 OR logg_gspspec>=3.6 ) AND ((flags_gspspec LIKE '____________0%') OR (flags_gspspec LIKE '____________1%')) AND ((flags_gspspec LIKE '0%') OR (flags_gspspec LIKE '1%')) AND ((flags_gspspec LIKE '_0%') OR (flags_gspspec LIKE '_1%')) AND ((flags_gspspec LIKE '__0%') OR (flags_gspspec LIKE '__1%')) AND ((flags_gspspec LIKE '___0%') OR (flags_gspspec LIKE '___1%')) AND ((flags_gspspec LIKE '____0%') OR (flags_gspspec LIKE '____1%')) AND((flags_gspspec LIKE '_____0%') OR (flags_gspspec LIKE '_____1%')) AND ((flags_gspspec LIKE '______0%') OR (flags_gspspec LIKE '______1%') OR (flags_gspspec LIKE '______2%') OR (flags_gspspec LIKE '______3%')) AND ((flags_gspspec LIKE '_______0%') OR (flags_gspspec LIKE '_______1%') OR (flags_gspspec LIKE '_______2%'))
Reflectance spectra of Main Belt small bodies
Use case: I want to retrieve the wavelengths, reflectances, and reflectance errors for the asteroid numbered 21 by the Minor Planet Center (Reflectance spectra of Main Belt small bodies, Gaia Data Release 3: Reflectance spectra of solar system small bodies).
Target table: gaiadr3.gaia_source, gaiadr3.astrophysical_parameters
Query:
SELECT wavelength, reflectance_spectrum, reflectance_spectrum_err FROM gaidr3.sso_reflectance_spectrum WHERE number_mp = 21
Radial-velocity variable stars
Use case: I want to identify radial-velocity variable stars applying the criteria described in Gaia Data Release 3: Properties and validation of the radial velocities.
Target table: gaiadr3.gaia_source
Query:
SELECT * FROM gaiadr3.gaia_source WHERE rv_nb_transits >= 10 AND rv_template_teff BETWEEN 3900 AND 8000 AND rv_chisq_pvalue <= 0.01 AND rv_renormalised_gof > 4
Stellar multiplicity, a teaser for the hidden treasure
Use case: I want to compare orbital periods from the "gaiadr3.nss_two_body_orbit" table against photometric periods from the "gaiadr3.vari_long_period_variable" table. Adapted from Gaia Data Release 3: Stellar multiplicity, a teaser for the hidden treasure.
Target tables: gaiadr3.nss_two_body_orbit, gaiadr3.vari_long_period_variable
Query:
SELECT * FROM gaiadr3.nss_two_body_orbit AS TBO, gaiadr3.vari_long_period_variable AS LPV WHERE LPV.source_id = TBO.source_id AND LPV.frequency IS NOT NULL
Gaia DR2 sElected queries
Light Curves / epoch photometry
Use case: I want to retrieve the light curves for two variable stars (DR2, Gaia Collaboration, Holl et al. 2018 A&A 618, A30; adapted Fig. A1).
Target table: gaiadr2.gaia_source, gaiadr2.vari_rrlyrae, gaiadr2.vari_long_period_variable, gaiadr2.vari_classifier_result
Query:
SELECT gaia.source_id, phot_variable_flag, best_class_name, datalink_url, sosrrl.pf, sosrrl.epoch_g, soslpv.frequency FROM gaiadr2.gaia_source AS gaia LEFT OUTER JOIN gaiadr2.vari_classifier_result AS variables USING (source_id) LEFT OUTER JOIN gaiadr2.vari_rrlyrae AS sosrrl USING (source_id) LEFT OUTER JOIN gaiadr2.vari_long_period_variable AS soslpv USING (source_id) WHERE gaia.source_id IN (1372970619261887104, 5368939678153068288)
Density distribution of radial velocities
Use case: I want to show the average distribution of Gaia DR2 radial velocities in Galactic Coordinates (DR2, Gaia Collaboration, Katz et al. 2019 A&A 622, A205; adapted Fig. 7).
Target table: gaiadr2.gaia_source
Query:
SELECT GAIA_HEALPIX_INDEX(6, source_id) AS healpix6, AVG(radial_velocity) AS avg_radial_velocity FROM gaiadr2.gaia_source WHERE radial_velocity IS NOT NULL GROUP BY healpix6
Observed CMD diagram
Use case: I want to construct an observed CMD diagram (DR2, Gaia Collaboration, Andrae et al. 2018 A&A 616, A8; adapted Fig. 19).
Target table: gaiadr2.gaia_source
Query:
SELECT bp_rp_index / 40 AS bp_rp, g_abs_index / 10 AS g_abs, n FROM ( SELECT FLOOR(bp_rp * 40) AS bp_rp_index,FLOOR((phot_g_mean_mag + 5 * LOG10(parallax) - 10) * 10) AS g_abs_index, COUNT(*) AS n FROM gaiadr2.gaia_source WHERE parallax_over_error > 5 AND a_g_val IS NOT NULL AND random_index < 800000 GROUP BY bp_rp_index, g_abs_index ) AS subquery
Average Extinction distribution
Use case: I want to obtain the parallax-averaged A_G Extinction (DR2, Gaia Collaboration, Andrae et al. 2018 A&A 616, A8; adapted Fig. 21).
Target table: gaiadr2.gaia_source
Query:
SELECT GAIA_HEALPIX_INDEX(8, source_id) AS healpix8, AVG(a_g_val) AS avg_a_g_val FROM gaiadr2.gaia_source WHERE a_g_val IS NOT NULL AND random_index < 800000 GROUP BY healpix8
Extinction towards Orion
Use case: I want to obtain the extinction towards Orion for a distance slice between 0.6 AND 1.0 kpc (DR2, Gaia Collaboration, Andrae et al. 2018 A&A 616, A8; adapted Fig. 34).
Target table: gaiadr2.gaia_source
Query:
SELECT l_index / 2 AS l, b_index / 4 AS b, extinction, n FROM ( SELECT FLOOR((l - 360) * 2) AS l_index, FLOOR(b * 4) AS b_index, AVG(a_g_val) AS extinction, COUNT(*) AS n FROM gaiadr2.gaia_source WHERE l BETWEEN 180 AND 230 AND b BETWEEN -25 AND 0 AND parallax_over_error > 5 AND a_g_val IS NOT NULL AND parallax BETWEEN 1. AND 1. / 0.6 AND random_index < 800000 GROUP BY l_index, b_index ) AS subquery
RR Lyrae sky density distribution.
Use case: I want to retrieve the sky density distribution of RR Lyrae stars (DR2, Gaia Collaboration, Holl et al. 2018 A&A 618, A30; adapted Fig. 6).
Target table: gaiadr2.gaia_source
Query:
SELECT GAIA_HEALPIX_INDEX(6, source_id) AS healpix6, COUNT (*)/ 0.9161 AS stars_per_sq_deg FROM gaiadr2.vari_classifier_result WHERE best_class_name='RRAB' OR best_class_name='RRC' OR best_class_name='RRD' OR best_class_name='ARRD' GROUP BY healpix6
Gaia DR1 sElected queries
Gaia DR1-2MASS HR diagram
Use case: I want to construct the Gaia DR1-TMASS HR diagram (DR1, Gaia Collaboration, Brown Holl et al. 2016 A&A 595, A2; adapted Fig. 5).
Target table: gaiadr1.gaia_source, gaiadr1.tmass_best_neighbour, gaiadr1.tmass_original_valid
Query:
SELECT TOP 100 gaia.source_id, gaia.phot_g_mean_mag + 5 * LOG10(gaia.parallax) - 10 AS g_mag_abs, gaia.phot_g_mean_mag - tmass.ks_m AS g_min_ks FROM gaiadr1.gaia_source AS gaia INNER JOIN gaiadr1.tmass_best_neighbour AS xmatch USING (source_id) INNER JOIN gaiadr1.tmass_original_valid AS tmass USING (tmass_oid) WHERE gaia.parallax/gaia.parallax_error >= 5 AND ph_qual = 'AAA' AND SQRT(POWER(2.5 / LOG(10) * gaia.phot_g_mean_flux_error / gaia.phot_g_mean_flux, 2) ) <= 0.05 AND SQRT(POWER(2.5 / LOG(10) * gaia.phot_g_mean_flux_error gaia.phot_g_mean_flux, 2) + POWER(tmass.ks_msigcom, 2)) <= 0.05
Gaia DR1-2MASS HR diagram
Use case: I want to construct the Gaia DR2 HR diagram. (DR1, Gaia Collaboration, Brown Holl et al. 2016 A&A 595, A2; adapted Fig. 5).
Target table: gaiadr1.gaia_source
Query:
SELECT g_min_ks_index / 10 AS g_min_ks, g_mag_abs_index / 10 AS g_mag_abs, COUNT(*) AS n FROM ( SELECT TOP 100 gaia.source_id, FLOOR((gaia.phot_g_mean_mag+5*LOG10(gaia.parallax)-10) * 10) AS g_mag_abs_index, FLOOR((gaia.phot_g_mean_mag-tmass.ks_m) * 10) AS g_min_ks_index FROM gaiadr2.gaia_source AS gaia INNER JOIN gaiadr2.tmass_best_neighbour AS xmatch USING (source_id) INNER JOIN gaiadr1.tmass_original_valid AS tmass USING (tmass_oid) WHERE gaia.parallax/gaia.parallax_error >= 5 AND ph_qual = 'AAA' AND SQRT(POWER(2.5 / LOG(10) * gaia.phot_g_mean_flux_error / gaia.phot_g_mean_flux, 2)) <= 0.05 AND SQRT(POWER(2.5 / LOG(10) * gaia.phot_g_mean_flux_error / gaia.phot_g_mean_flux, 2) + POWER(tmass.ks_msigcom, 2)) <= 0.05 ) AS subquery GROUP BY g_min_ks_index, g_mag_abs_index
Cepheids: light curve retrieval for all stars
Use case: I want to retrieve complete epoch photometry of a given object class for offline analysis (DR1, Gaia Collaboration, Clementini et al. 2016 A&A 595, A133).
Notes: After DR1 light curves are provided via DataLink interface (see dedicated Tutorial).
Target table: gaiadr1.cepheid, gaiadr1.phot_variable_time_series_gfov
Query:
SELECT gaia.* FROM gaiadr1.phot_variable_time_series_gfov AS gaia INNER JOIN gaiadr1.cepheid AS cep USING (source_id)
RR Lyrae: phase-folded light curve reconstruction, including errors
Use case: I want to construct a phase-folded light curve for comparison to stars with different periods (DR1, Gaia Collaboration, Brown et al. 2016 A&A 595, A2; adapted Fig. 7).
Notes: After Gaia DR1, light curves are being provided via the DataLink interface (see dedicated Tutorial).
Target table: gaiadr1.rrlyrae, gaiadr1.phot_variable_time_series_gfov
Query:
SELECT curves.observation_time, MOD(curves.observation_time - rrlyrae.epoch_g, rrlyrae.p1)/ rrlyrae.p1 AS phase, curves.g_magnitude, 2.5 / log(10) * curves.g_flux_error / curves.g_flux AS g_magnitude_error FROM gaiadr1.phot_variable_time_series_gfov AS curves INNER JOIN gaiadr1.rrlyrae AS rrlyrae USING (source_id) WHERE rrlyrae.source_id = 5284240582308398080
RR Lyrae: number of data points and estimated parameters
Use case: I want high-level information for a given class of variable objects (DR1, Gaia Collaboration, Clementini et al. 2016 A&A 595, A133).
Notes: After Gaia DR1, light curves are being provided via the DataLink interface (see dedicated Tutorial).
Target table: gaiadr1.rrlyrae, gaiadr1.phot_variable_time_series_gfov_statistical_parameters
Query:
SELECT stat.num_observations_processed, rr.* FROM gaiadr1.phot_variable_time_series_gfov_statistical_parameters AS stat INNER JOIN gaiadr1.rrlyrae AS rr USING (source_id)
