Science nugget: Measuring the nascent solar wind outflow velocities via the doppler dimming technique - Solar Orbiter

MEASURING THE NASCENT SOLAR WIND OUTFLOW VELOCITIES VIA THE DOPPLER DIMMING TECHNIQUE

(Solar Orbiter nugget #7 by Daniele Spadaro¹, Daniele Telloni²and the METIS team)

Doppler dimming

Some strong lines in the EUV/UV spectral range are known to be visible in the solar corona up to several solar radii above the limb, e.g., the H I Lyα at 121.6 nm and the O VI doublet at 103.2 and 103.7 nm, both observed with UVCS onboard SOHO [1, 2]. These spectral lines are very suitable for the study of the dynamic properties of the continuously expanding corona, which is important for gaining insight into the origin of the solar wind and the creation of the heliosphere. Indeed, an expanding corona causes, as described in more detail below, the intensity of these lines to decrease.

They are mainly excited by the disk radiation through the resonant scattering of incoming photons by the neutral atoms and ions in the corona, since the contribution from free-electron collisions is negligible due to the very rarefied external solar atmosphere. For instance, the HI Lyα observed in the extended corona is mainly formed by the resonant scattering of chromospheric Lyα photons by neutral hydrogen atoms in the corona [3].

The intensity of a coronal resonance line depends on the number of particles in the line of sight that are able to scatter radiation in the line, i.e., on the local state of the coronal plasma (electron density ne, temperature Te, elemental abundance Ael, neutral atom/ion kinetic temperature THI,i), and on the intensity and profile of the incoming radiation from the solar disk and lower levels of the corona.

The number of scatterings also depends on the outflow velocity of the solar plasma. In a static atmosphere, the central wavelength of the coronal scattering line profile is identical to that of the disk profile. However, in a region with solar wind flow, the Lyα disk profile is Doppler-shifted (red-shifted) with respect to the coronal scattering profile (see Figure 1), so that there is less efficient scattering resulting in a reduction in intensity of the scattered radiation, that decreases as the flow velocity increases. This effect is known as Doppler dimming (see [4], [5]). There are a variety of techniques for determining the amount of Doppler dimming, that have been extensively described by different authors ([6], [7] and [8]).

If the outflow velocity of emitting atoms is high enough (i.e., > 4 − 500 km/s [7]), excitation and absorption profiles are completely Doppler-shifted, the scattered radiation totally dimmed and the corona becomes invisible at the wavelength of 121.6 nm.

Spectroscopic observations of the UV solar corona and, particularly, measurements of the intensity of the HI Lyα, can thus be used in conjunction with visible light observations of the coronal polarized brightness to probe the speed of the expanding coronal plasma. The outflow velocity in the solar corona is generally derived by the comparison of the observed resonantly scattered UV emission with the emission calculated adopting the electron density, ne. The latter is determined from the observed polarized brightness by means of the inversion technique (initially developed by [9]) and a suitable set of values of the other physical parameters as input data in the synthesis computation (see, e.g. [10, 11]). The intensity depends on the only free parameter, the outflow velocity, whose value is returned iteratively until a satisfactory match between the calculated and observed intensities is reached.

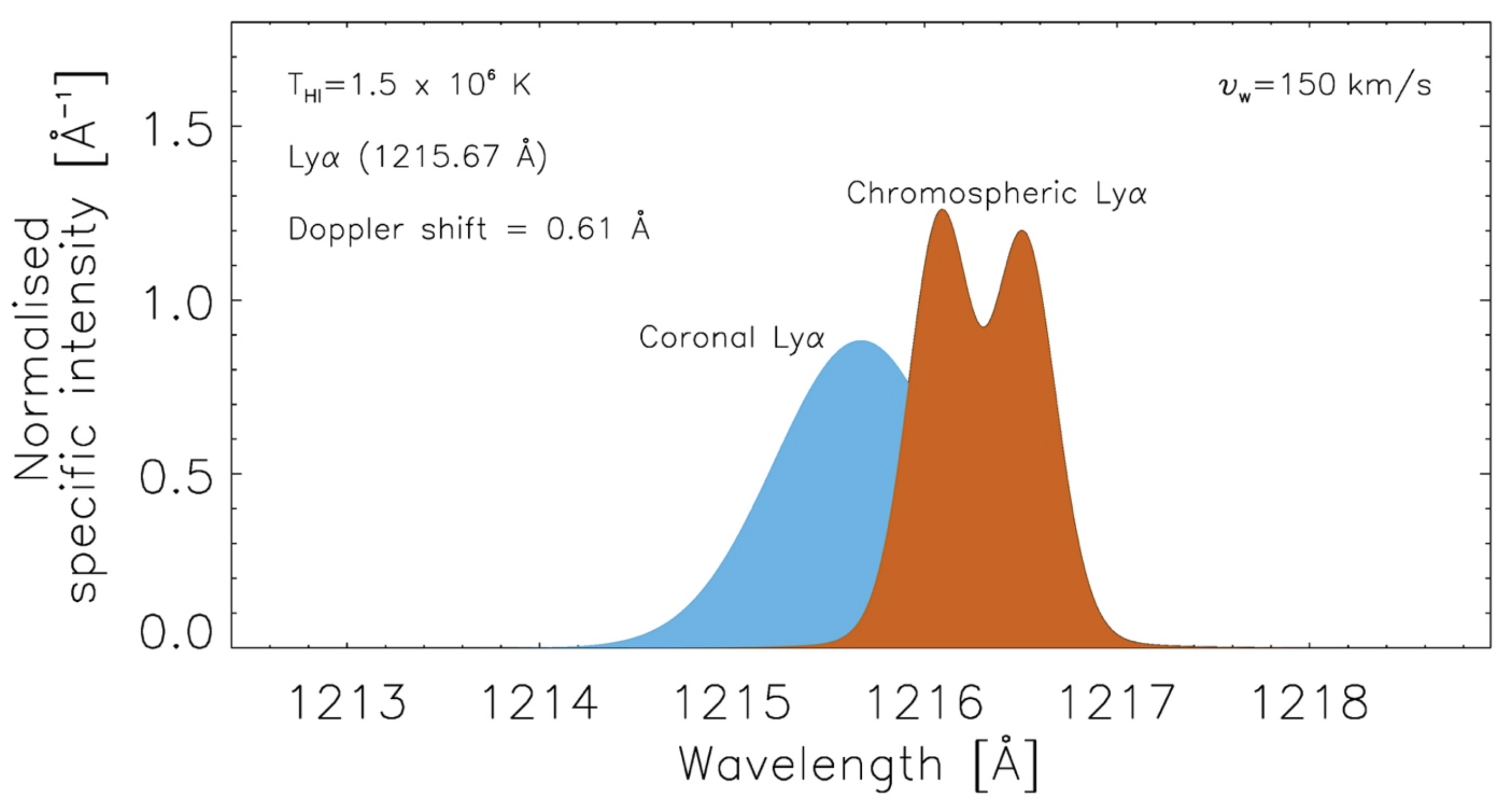
Figure 1: Doppler shift of the chromospheric Lyα profile with respect to the coronal Lyα profile for an outflow velocity value of 150 km/s. The Gaussian coronal profile is calculated for a neutral hydrogen kinetic temperature equal to 1.5 MK.

From UVCS to Metis

The Doppler dimming technique described here has been extensively used in the analysis of UVCS/SOHO spectroscopic data to characterize the solar wind physical properties in its early development (see, e.g., [12, 13, 14]). The study of UVCS data over more than one solar cycle has provided insights into the range of coronal heights where the fast solar wind originating from coronal holes is mostly accelerated (the reader is referred to the review [15] and the references therein), as well as the origin of the slow solar wind [16], thus finally yielding clues about coronal heating processes.

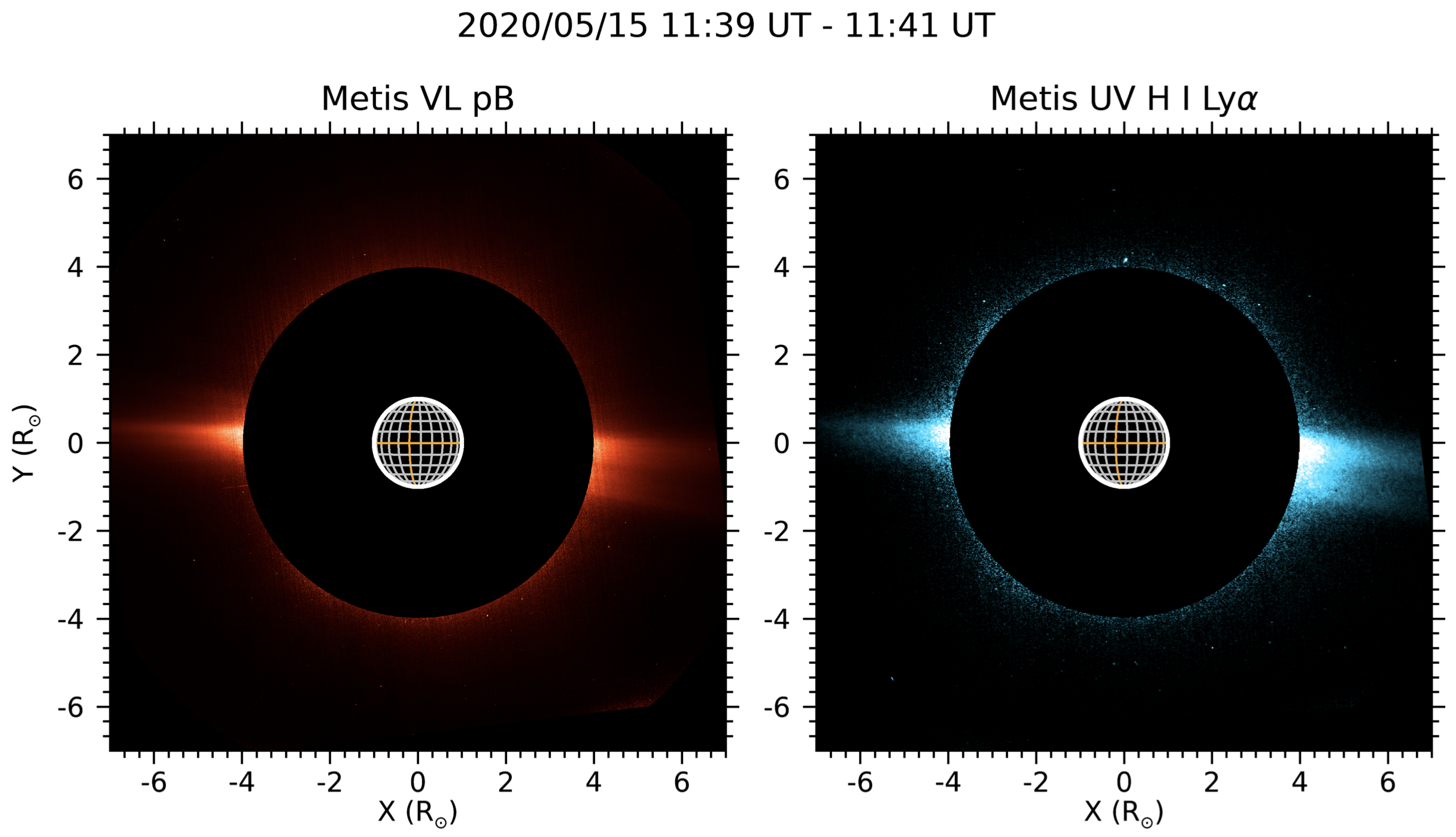
Figure 2: Visible-light polarized brightness within 580 − 640 nm band (left panel) and ultraviolet HI Lyα emission at 121.6 nm (right panel) of the solar corona observed from a vantage point of 0.64 AU on May 15, 2020, at 11:40 UT, within a field-of-view ranging from 3.8 R⊙ to 7 R⊙. From [10].

Outflow velocity determination algorithms have been recently developed for the application of the Doppler dimming technique to the observations performed by the Metis coronagraph [17] onboard Solar Orbiter [18]. Details are reported in [19, 20, 17, 11, 21, 10, 22, 23]. In [19, 20] in particular, the authors investigated the dependence of the derived outflow velocities on the values of the physical quantities representative of the coronal environment adopted in the synthesis of the resonantly scattered HI Lyα line intensity. They found that the coronal electron temperature and the HI kinetic temperature, as well as the chromospheric Lyα brightness distribution, have the greatest influence on the outflow velocity derivation. Also, the assumption of isotropic or anisotropic kinetic temperature for the hydrogen atoms significantly affects the determination of the solar wind outflow velocities, as recently shown in [10] and [11]. These authors specifically used the first observations performed by the Metis coronagraph aboard Solar Orbiter on May 15, 2020 during the cruise phase, simultaneously imaging the polarized visible light and the HI Lyα corona (see Figure 2), to obtain the first instantaneous maps of the speed of the coronal plasma outflows along the equatorial streamer belt during the minimum of solar activity (see Figure 3). The wind thus imaged is the slow coronal flow originating from low-latitude coronal regions. Whether the low-speed streams originate primarily from the streamer cups or from the boundary regions of coronal holes and equatorial streamers is still an open question, which Metis wil lanswer. Later observations were then also used to investigate the fast solar wind emerging from polar coronal holes during a solar minimum-type magnetic configuration [23].

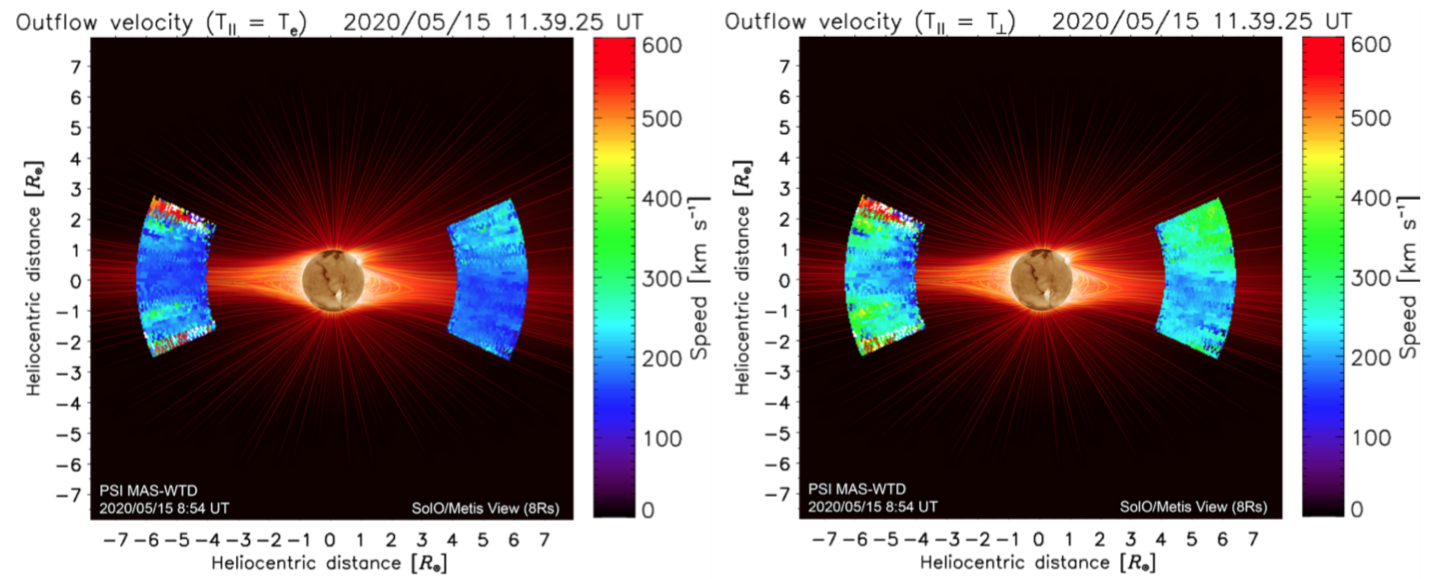
Figure 3: HI outflow velocity map, within the region where the S/N is equal to 5, in the case of anisotropy, THI,∥ = Te (left panel) and of isotropy THI,∥ = THI,⊥ (right panel) of the neutral hydrogen kinetic temperature along the radial direction. From [10].

Conclusion

The Doppler dimming techniques described above provide a means of obtaining information on outward flow velocities, as well as mass flux, as a function of height above the solar limb and of solar latitude, including the polar regions. Indeed, in the regions below approximately 10 solar radii, where the time for hydrogen-proton charge exchange is less than the coronal expansion time [24, 25], the neutral hydrogen flow traces that of protons which are the species carrying most of the mass of the solar wind and thus represent the main component of the coronal plasma. This results in a sensitive determination of the magnitude and location of the solar wind acceleration near the Sun, that is useful to locate and characterize the coronal source regions of the solar wind, and to identify and understand the dominant physical processes that accelerate it. Future studies based on the Metis observations will hence contribute significantly to addressing long-standing questions, such as the origin of the slow solar wind, how the magnetic field configuration modulates the speed of coronal flows, or what mechanisms underlie the heating and subsequent acceleration of the solar wind.

Affiliations:

(1) National institute for Astrophysics, Astrophysical Observatory of Catania, Via Santa Sofia 78, I-95123 Catania, Italy

(2) National institute for Astrophysics, Astrophysical Observatory of Torino, Via Osservatorio 20, I-10025 Pino Torinese, Italy

References

[1] Kohl, J. L., Esser, R., Gardner, L. D., et al. 1995, Solar Physics, 162(1-2), 313–356.

[2] Kohl, J. L., Noci, G., Antonucci, E., et al., 1997, Solar Physics, 175(2), 613–644.

[3] Gabriel, A. H., 1971, Solar Physics, 21(2), 392–400.

[4] Hyder, C. L., & Lites, B. W., 1970, Solar Physics, 14(1), 147–156.

[5] Beckers, J. M., & Chipman, E., 1974, Solar Physics, 34(1), 151–161.

[6] Kohl, J. L., & Withbroe, G. L., 1982, The Astrophysical Journal, 256, 263–270.

[7] Withbroe, G. L., Kohl, J. L., Weiser, H., & Munro, R. H., 1982, Space Science Reviews, 33(1-2), 17–52.

[8] Noci, G., Kohl, J. L., & Withbroe, G. L., 1987, The Astrophysical Journal, 315, 706.