IoW_20200722 - Gaia

Image of the Week

Gaia and the size of the Solar system

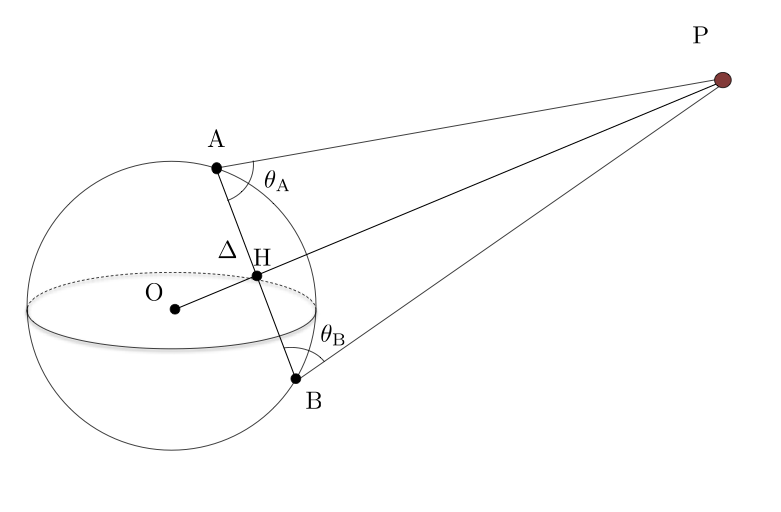
Figure 1: Distance of a solar system body by triangulation on the Earth. Two observers in A and B perform astronomical sights to the planet P to get the two angles at A and B. The distance of the baseline AB is known from a combination of astronomical and geodetic measurements. The distance to the planet is computed by resolving the triangle with simple trigonometry. Image source : GAIA-C4-TN-OCA-FM-061

1 - Objective and principles

If one asks anyone familiar with Gaia what the spacecraft and the DPAC scientists are doing, chances are that the answer will mention the Milky Way, the positions and distances of the stars, the quasars rather than the size of the solar system. Undoubtedly the mission has been shaped out to explore firstly the stellar world, but also the positions of small bodies in the solar system, but in no case to estimate the distance to the Sun. This is a topic outside the scope of Gaia, and above all, since 2012 the astronomical unit (au) is a defining constant of the system of units used by astronomers and for this reason no longer the subject of measurements.

However in 2019 and 2020, the minor planets Eros and 1998 OR2 came relatively close to the Earth, at less than one fourth of the distance to the Sun. This fortunate feature has allowed Gaia scientists to repeat on a grander scale a technique used by astronomers of the past centuries (actually until 1950, not long ago) to find the true scale of the solar system. Not really for science, this scale is well known today, but for the purpose of education and stressing a fundamental principle of Gaia, the aptly named trigonometric triangulation, put into operation in a simpler framework than with the stars.

Hence in this story, unlike most others published on the Gaia website, there is no cutting-edge science derived from Gaia data, but just the revival of an old-fashioned technique to ascertain distances in the Solar system. Likewise, this offers an opportunity to provide students, teachers, young astronomers, historians of astronomy, data scientists with observations carried out with a spacecraft to train in astrometry, astronomical computing, data analysis with the pleasure of finding a result that would have been a top level publication in 1960, not that far in the past for astronomers.

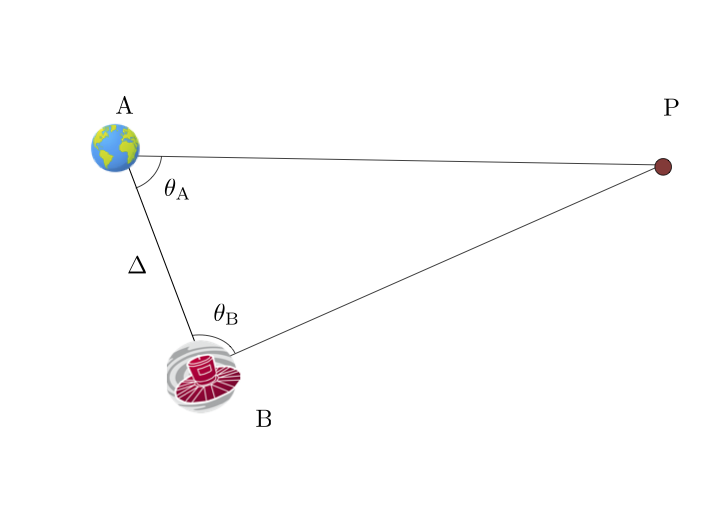
Figure 2. Triangulation of a minor planet between the Earth and Gaia. Same as in Fig. 1, but with a much larger baseline of 1.5 million kilometres. Image source : GAIA-C4-TN-OCA-FM-061

2- Triangulation in astronomy

The principle of measurement put into its simplest form is just a trigonometric resolution of a triangle and has been known for centuries. It was applied by Hipparchus to the Moon, before it was effectively used for the solar parallax in the XVIIth century by J.D. Cassini in Paris and J. Flamsteed in London and successfully extended to the stars by F.W. Bessel in the XIXth century. Today this is the ground technique employed by Gaia to gauge the Universe.

The principle is illustrated in Figure 1, with two observers located in A and B measuring the direction of a planet at P. Given the finite distance to the planet, the two lines AP and BP are not parallel to each other, and the angles in A and B are slightly different. The larger the baseline AB, the bigger the difference between the two angles. But the solar system is big compared to the size of the Earth, and the figure is not to scale. In every practical case met in the past, the angle at P was always small, if not very small, at most 100 seconds of an arc in the most favourable circumstances. Unfortunately one cannot play with the distance of the planets, but can we have a bigger baseline to increase the angle P?

This is where Gaia comes into play. Replace one of the observers by Gaia as in Figure 2, and all of a sudden the baseline grows from less than 10,000 km to 1.5 million km, while the angle at P goes up to several degrees. A factor 150 almost for free, given the fact that no particular constraint is requested from the Gaia operations. Gaia is scanning the sky and the planetary targets are found within the normal programme by mining the data flow.

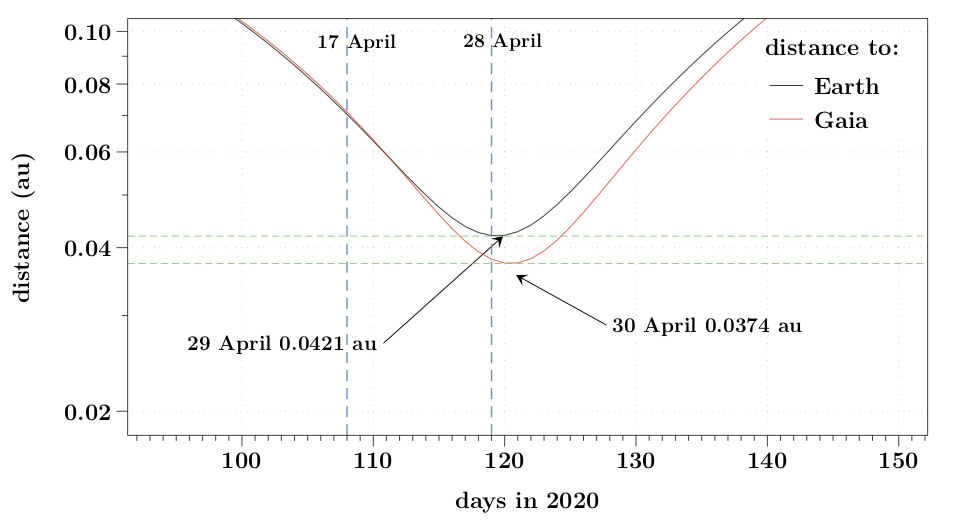
Figure 3. Distance to the Earth and to Gaia of 1998 OR2 around its fly-by. The vertical dashed lines indicate the date of the Gaia observations. Image source : GAIA-C4-TN-OCA-FM-061

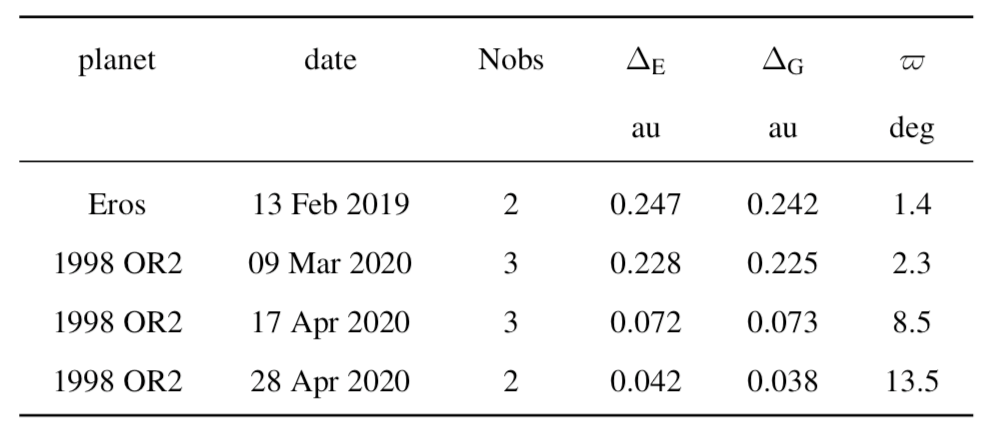
3 - Gaia observations

We were fortunate that Gaia observed both Eros and 1998 OR2 several times during the oppositions of 2019 and 2020, and by a stroke of chance for 1998 OR2, within days of its closest approach, as it can be seen in Figure 3. Altogether there were 10 successful on-board detections over four epochs given in Table 1. Thanks to the performance of the Gaia finder, one has relatively good positions (0.06" accuracy) at each passage, quickly available internally for the Gaia sanity monitoring. This data is normally for internal use and not made public. But given the interest of this project for education, these positions have been made accessible through the Minor Planet Center (MPC) and in this document.

Table 1: Passages of Eros and 1998 OR2 observed with Gaia in 2019 and 2020. Nobs is the number of detected transits with Gaia during the passage. ∆E and ∆G are the distances to the Earth and to Gaia. The last column is the parallactic angle. Table source : GAIA-C4-TN-OCA-FM-061

It is important to stress that the detection accuracy is not, and by far, the final Gaia astrometric accuracy for these observations (better than 1 mas) that won't be available before 2024 when the full processing of the 2019-2020 observations is completed. However this accuracy is largely enough for our purpose, and even better than the observations done on the Earth.

Ground-based observers being stimulated by the close approaches of asteroids, there is a large number of observations stored in the MPC system, giving the time of observation, the location of the observer and the recorded position of the planets. None is exactly synchronous with Gaia, but it was possible to interpolate within a day to get approximate Earth-centred observations at the same times as Gaia. The animation provided below (from Paolo Tanga, who is in charge of the Solar system group for Gaia) shows the displacement of 1998 OR2 over several hundreds of seconds on 16 April 2020. These observations have been added to the MPC dataset for this analysis.

The passage of Eros is particularly significant given its relationship with the historical measurements of the astronomical unit. Until 1965, the two close approaches of Eros in 1901 (at 0.31 au) and 1931 (at 0.17 au) provided the best estimates of the solar parallax. In particular the value derived by Sir Harold Spencer-Jones in 1941 from the data collected 10 years earlier, remained the IAU reference value until 1968. The extensive discussion of thousands of measurements yielded a solar parallax of 8.790" ± 0.001", or equivalently 149.65 million kilometres for the mean Sun-Earth distance. The true error was in fact four times larger, giving a relative accuracy of about 0.0005. This was the best that could be achieved with the participation of 24 observatories over the world and nearly 3000 photographic plates with multiple images of Eros. It took 10 years to complete the analysis and reach a consensus about the size of the solar system. A simple principle may hide dreadful complexity in the details.
 

The asteroid (52768) 1998 OR2 imaged through a 35 cm telescope close to its flyby with the Earth, on the evening of April 16, 2020. A sequence of hundreds of images taken 4 seconds apart have been assembled to create this animation, showing the motion of the nearby asteroid among the background stars. The sequence, which real duration is about 20 minutes, has been accelerated 200 times. Credits: P. Tanga, Observatoire de la Côte d'Azur (France); editing: G. Peretti, Torino (Italy).

4. Data analysis and result

The data analysis is rather straightforward and described in detail here. In Figure 2, by means of celestial mechanics, one can compute the paths of the minor planets with great accuracy with the distances expressed with the Earth-Sun distance as a yardstick. Therefore the length AP is known directly in astronomical units.

Now the baseline AB comes out naturally in km from the spacecraft regular tracking by ESOC experts, using Doppler technique or direct ranging. The measurements of the angles at A and B, combined with the baseline, allows us to resolve the triangle by simple trigonometry, and then compute AP in kilometres. By comparing to the same distance in astronomical unit, one deduces the value of the latter in kilometres. That's all!

The only small technical complication comes from the need to carry apparent directions obtained at the surface of the Earth, to the corresponding directions at the centre of the Earth, as if there were observers there taking sights of the planets. This needs the conversion between kilometres (station position on the Earth) to astronomical units (distance to the planet), but the required scale factor is precisely the goal of the whole project! So one must start from an approximate value and iterate, since this effect is just a correction. The whole procedure converges quickly and one can initially neglect this effect or, equivalently, place the planet at very large distance in comparison to the radius of the Earth.

At the end, the ten observations of Eros and that of 1998 OR2 give a solar parallax or the mean Sun-Earth distance to better than 0.00001 in relative error, about 50 times better than the best historical measurement relying on this technique, published in 1941. While this achievement is of no importance for contemporary science, it would have been a remarkable result in 1960.

Today, the only purpose of taking time to process this data should be to train young astronomers, physics teachers, historians of astronomy, and students in statistics to experiment with real data and see the difference between a very simple geometric principle and its use in the real world. Having large angles permits (almost) anyone interested to find the size of the solar system, but without dealing with the technical difficulties that arise when one has to deal with small angles. However, this is a very nice opportunity to link modern and historical techniques, to appreciate how real science is done, and for anyone to make ones own pathway in the art of astronomical computing.

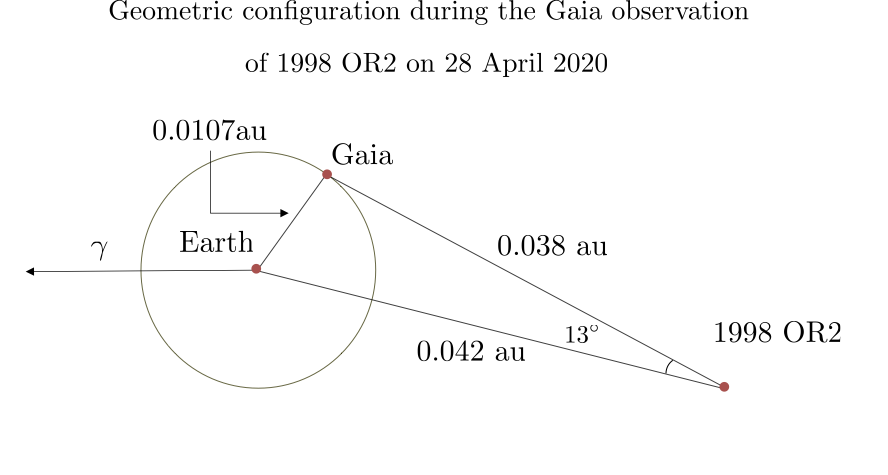
Figure 4. Geometric configuration between the Earth, Gaia, and the planet 1998 OR2 during the Gaia observation of 28 April 2020. The large parallactic angle of 13 degrees is unique in the history of astronomy in the determination of the solar parallax. Image source : GAIA-C4-TN-OCA-FM-061

Further reading:

The Solar Parallax with Gaia / GAIA-C4-TN-OCA-FM-061

Credits: ESA/Gaia/DPAC, F. Mignard, P. Tanga, B. Carry, M. Delbo, L. Galluccio, F. Spoto, DPAC members at the Observatoire de la Côte d'Azur in Nice & and CfA/Harvard & Smithsonian (FS)

[Published: 22/07/2020]